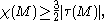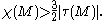Hitchin–Thorpe inequality
Encyclopedia
In differential geometry the Hitchin–Thorpe inequality is a famous relation which restricts the topology of 4-manifold
s that carry an Einstein metric
.
where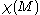 is the Euler characteristic
is the Euler characteristic
of and
and 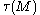 is the signature of
is the signature of 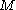 . This inequality was first stated by John Thorpe in a footnote to a 1969 paper focusing
. This inequality was first stated by John Thorpe in a footnote to a 1969 paper focusing
on manifolds of higher dimension. Nigel Hitchin
then rediscovered the inequality, and gave a complete characterization of the equality case in 1974; he found that if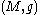 is an Einstein manifold with
is an Einstein manifold with 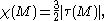 then
then 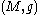 must be a flat torus, a Calabi–Yau manifold, or a quotient thereof.
must be a flat torus, a Calabi–Yau manifold, or a quotient thereof.
of the Riemann curvature tensor
and the Generalized Gauss-Bonnet theorem
.
Andrea Sambusetti independently showed that the answer is no: there exist infinitely many non-homeomorphic compact, smooth, oriented 4-manifolds M that carry no Einstein metrics but nevertheless satisfy
LeBrun's examples are actually simply connected, and the relevant obstruction depends on the smooth structure of the manifold. By contrast, Sambusetti's obstruction only applies to 4-manifolds with infinite fundamental group, but the volume-entropy estimate he uses to prove non-existence only depends on the homotopy type of the manifold.
4-manifold
In mathematics, 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different...
s that carry an Einstein metric
Einstein manifold
In differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
.
Statement of the Hitchin–Thorpe inequality
Let M be a compact, oriented, smooth four-dimensional manifold. If there exists a Riemannian metric on M which is an Einstein metric, then following inequality holdswhere
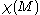 is the Euler characteristic
is the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of
 and
and 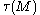 is the signature of
is the signature of 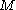 . This inequality was first stated by John Thorpe in a footnote to a 1969 paper focusing
. This inequality was first stated by John Thorpe in a footnote to a 1969 paper focusingon manifolds of higher dimension. Nigel Hitchin
Nigel Hitchin
Nigel Hitchin is a British mathematician working in the fields of differential geometry, algebraic geometry, and mathematical physics.-Academic career:...
then rediscovered the inequality, and gave a complete characterization of the equality case in 1974; he found that if
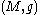 is an Einstein manifold with
is an Einstein manifold with 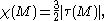 then
then 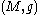 must be a flat torus, a Calabi–Yau manifold, or a quotient thereof.
must be a flat torus, a Calabi–Yau manifold, or a quotient thereof.Idea of the proof
The main ingredients in the proof of the Hitchin–Thorpe inequality are the decompositionRicci decomposition
In semi-Riemannian geometry, the Ricci decomposition is a way of breaking up the Riemann curvature tensor of a pseudo-Riemannian manifold into pieces with useful individual algebraic properties...
of the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
and the Generalized Gauss-Bonnet theorem
Generalized Gauss-Bonnet theorem
In mathematics, the generalized Gauss–Bonnet theorem presents the Euler characteristic of a closed even-dimensional Riemannian manifold as an integral of a certain polynomial derived from its curvature...
.
Failure of the converse
A natural question to ask is whether the Hitchin–Thorpe inequality provides a sufficient condition for the existence of Einstein metrics. In 1995, Claude LeBrun andAndrea Sambusetti independently showed that the answer is no: there exist infinitely many non-homeomorphic compact, smooth, oriented 4-manifolds M that carry no Einstein metrics but nevertheless satisfy
LeBrun's examples are actually simply connected, and the relevant obstruction depends on the smooth structure of the manifold. By contrast, Sambusetti's obstruction only applies to 4-manifolds with infinite fundamental group, but the volume-entropy estimate he uses to prove non-existence only depends on the homotopy type of the manifold.