Holomorphically convex hull
Encyclopedia
In mathematics
, more precisely in complex analysis
, the holomorphically convex hull of a given compact set in the n-dimension
al complex
space Cn is defined as follows.
Let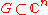
be a domain (an open
and connected set), or alternatively for a more general definition, let
be an 
dimensional complex analytic manifold. Further let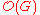 
stand for the set of holomorphic function
s on
For a compact set 
, the holomorphically convex hull of 
is
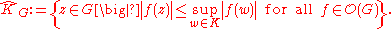
(One obtains a narrower concept of polynomially convex hull by requiring in the above definition that f be a polynomial
.)
The domain
is called holomorphically convex if for every 
compact in 
, 
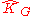is also compact in 
. Sometimes this is just abbreviated as holomorph-convex.
When
, any domain 
is holomorphically convex since then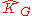 
is the union of 
with the relatively compact components of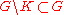 
. Also note that being holomorphically convex is the same as being a domain of holomorphy
(The Cartan–Thullen theorem). These concepts are more important in the case n > 1 of several complex variables
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more precisely in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, the holomorphically convex hull of a given compact set in the n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
space Cn is defined as follows.
Let
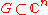be a domain (an openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
and connected set), or alternatively for a more general definition, let
be an dimensional complex analytic manifold. Further let 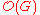stand for the set of holomorphic functionHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s on
For a compact set , the holomorphically convex hull of is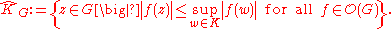(One obtains a narrower concept of polynomially convex hull by requiring in the above definition that f be a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
.)
The domain
is called holomorphically convex if for every compact in , 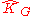is also compact in . Sometimes this is just abbreviated as holomorph-convex.When
, any domain is holomorphically convex since then 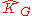is the union of with the relatively compact components of 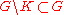. Also note that being holomorphically convex is the same as being a domain of holomorphyDomain of holomorphy
In mathematics, in the theory of functions of several complex variables, a domain of holomorphy is a set which is maximal in the sense that there exists a holomorphic function on this set which cannot be extended to a bigger set....
(The Cartan–Thullen theorem). These concepts are more important in the case n > 1 of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
.