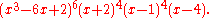Holt graph
Encyclopedia
In the mathematical
field of graph theory
, the Holt graph or Doyle graph is the smallest half-transitive graph
, that is, the smallest example of a vertex-transitive
and edge-transitive
graph which is not also symmetric
. Such graphs are not common. It is named after Peter G. Doyle and Derek F. Holt, who discovered the same graph independently in 1976 and 1981 respectively.
The Holt Graph has diameter 3, radius 3 and girth 5, chromatic number 3, chromatic index 5 and is Hamiltonian with distinct Hamiltonian cycles. It is also a 4-vertex-connected
and a 4-edge-connected
graph.
It has an automorphism group
of order 54 automorphisms. This is a smaller group than a symmetric graph with the same number of vertices and edges would have. The graph drawing on the right highlights this, in that it lacks reflectional symmetry.
The characteristic polynomial of the Holt graph is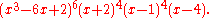
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Holt graph or Doyle graph is the smallest half-transitive graph
Half-transitive graph
In the mathematical field of graph theory, a half-transitive graph is a graph that is both vertex-transitive and edge-transitive, but not symmetric...
, that is, the smallest example of a vertex-transitive
Vertex-transitive graph
In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
and edge-transitive
Edge-transitive graph
In the mathematical field of graph theory, an edge-transitive graph is a graph G such that, given any two edges e1 and e2 of G, there is anautomorphism of G that maps e1 to e2....
graph which is not also symmetric
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
. Such graphs are not common. It is named after Peter G. Doyle and Derek F. Holt, who discovered the same graph independently in 1976 and 1981 respectively.
The Holt Graph has diameter 3, radius 3 and girth 5, chromatic number 3, chromatic index 5 and is Hamiltonian with distinct Hamiltonian cycles. It is also a 4-vertex-connected
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
and a 4-edge-connected
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
graph.
It has an automorphism group
Graph automorphism
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....
of order 54 automorphisms. This is a smaller group than a symmetric graph with the same number of vertices and edges would have. The graph drawing on the right highlights this, in that it lacks reflectional symmetry.
The characteristic polynomial of the Holt graph is