
Homogenization (mathematics)
Encyclopedia
In mathematics
and physics
, homogenization is the study of partial differential equations with rapidly oscillating coefficients,
such as

where is a very small parameter.
is a very small parameter.
In fact it turns out that the study of these equations are also of great importance in physics and engineering since equations of this type govern the physics of inhomogeneous or heterogeneous materials. Of course, all matter is inhomogeneous at some scale, but frequently it is convenient to treat it as homogeneous. A good example is the continuum concept which is used in continuum mechanics
. Under this assumption materials such as fluids, solids, etc. can be treated as homogeneous materials and associated with these materials are material properties such as shear modulus, elastic moduli, etc.
Frequently, inhomogeneous materials (such as composite materials) possess microstructure
and therefore they are subjected to loads or forcings which vary on a lengthscale which is far bigger than the characteristic lengthscale of the microstructure. In this situation, one can often replace the equation above with an equation of the form
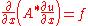
where is a constant and is known as the effective property associated with the material in question. This process of replacing an equation with a highly oscillatory coefficient with one with a homogeneous (uniform) coefficient is known as homogenization. This subject is inextricably linked with the subject of micromechanics
is a constant and is known as the effective property associated with the material in question. This process of replacing an equation with a highly oscillatory coefficient with one with a homogeneous (uniform) coefficient is known as homogenization. This subject is inextricably linked with the subject of micromechanics
for this very reason.
As a result of the above, homogenization can therefore be viewed as an extension of the continuum concept to materials which possess microstructure. The analogue of the differential element in the continuum concept (which contains enough atom, or molecular structure to be representative of that material), is known as the "Representative Volume Element" in homogenization and micromechanics. This element contains enough statistical information about the inhomogeneous medium in order to be representative of the material. Therefore averaging over this element gives an effective property such as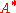 above.
above.
 and posing a formal expansion in
and posing a formal expansion in  :
:

which generates a hierarchy of problems. The homogenized equation is obtained and the effective coefficients are determined by solving the so-called "cell problems" for the function .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, homogenization is the study of partial differential equations with rapidly oscillating coefficients,
such as

where
 is a very small parameter.
is a very small parameter.In fact it turns out that the study of these equations are also of great importance in physics and engineering since equations of this type govern the physics of inhomogeneous or heterogeneous materials. Of course, all matter is inhomogeneous at some scale, but frequently it is convenient to treat it as homogeneous. A good example is the continuum concept which is used in continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
. Under this assumption materials such as fluids, solids, etc. can be treated as homogeneous materials and associated with these materials are material properties such as shear modulus, elastic moduli, etc.
Frequently, inhomogeneous materials (such as composite materials) possess microstructure
Microstructure
Microstructure is defined as the structure of a prepared surface or thin foil of material as revealed by a microscope above 25× magnification...
and therefore they are subjected to loads or forcings which vary on a lengthscale which is far bigger than the characteristic lengthscale of the microstructure. In this situation, one can often replace the equation above with an equation of the form
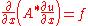
where
 is a constant and is known as the effective property associated with the material in question. This process of replacing an equation with a highly oscillatory coefficient with one with a homogeneous (uniform) coefficient is known as homogenization. This subject is inextricably linked with the subject of micromechanics
is a constant and is known as the effective property associated with the material in question. This process of replacing an equation with a highly oscillatory coefficient with one with a homogeneous (uniform) coefficient is known as homogenization. This subject is inextricably linked with the subject of micromechanicsMicromechanics
Micromechanics is the analysis of composite or heterogeneous materials on the level of the individual constituents that constitute these materials.- Aims of micromechanics of materials :...
for this very reason.
As a result of the above, homogenization can therefore be viewed as an extension of the continuum concept to materials which possess microstructure. The analogue of the differential element in the continuum concept (which contains enough atom, or molecular structure to be representative of that material), is known as the "Representative Volume Element" in homogenization and micromechanics. This element contains enough statistical information about the inhomogeneous medium in order to be representative of the material. Therefore averaging over this element gives an effective property such as
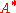 above.
above.The method of asymptotic homogenization
Mathematical homogenization theory dates back to the French, Russian and Italian schools. The method of asymptotic homogenization proceeds by introducing the fast variable and posing a formal expansion in
and posing a formal expansion in  :
:
which generates a hierarchy of problems. The homogenized equation is obtained and the effective coefficients are determined by solving the so-called "cell problems" for the function
 .
.

