Hosford yield criterion
Encyclopedia
The Hosford yield criterion is a function that is used to determine whether a material has undergone plastic yielding under the action of stress.
The Hosford yield criterion for isotropic materials is a generalization of the von Mises yield criterion. It has the form
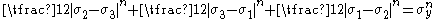
where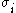
, i=1,2,3 are the principal stresses, 
is a material-dependent exponent and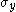 
is the yield stress in uniaxial tension/compression.
Alternatively, the yield criterion may be written as
This expression has the form of an Lp norm
which is defined as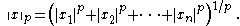
When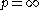
, the we get the L∞ norm,
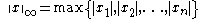. Comparing this with the Hosford criterion
indicates that if n = ∞, we have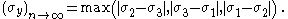
This is identical to the Tresca yield criterion.
Therefore, when n = 1 or n goes to infinity the Hosford criterion reduces to the Tresca yield criterion. When n = 2 the Hosford criterion reduces to the von Mises yield criterion.
Note that the exponent n does not need to be an integer.
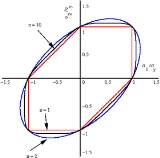
A plot of the yield locus in plane stress for various values of the exponent
is shown in the adjacent figure.
The Logan-Hosford yield criterion for anisotropic plasticity is similar to Hill's generalized yield criterion
and has the form
where F,G,H are constants,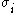
are the principal stresses, and the exponent n depends on the type of crystal (bcc, fcc, hcp, etc.) and has a value much greater than 2. Accepted values of 
are 6 for bcc materials and 8 for fcc materials.
Though the form is similar to Hill's generalized yield criterion
, the exponent n is independent of the R-value unlike the Hill's criterion.
where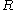
is the R-value and 
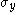is the yield stress in uniaxial tension/compression. For a derivation of this relation see Hill's yield criteria for plane stress. A plot of the yield locus for the anisotropic Hosford criterion is shown in the adjacent figure. For values of 
that are less than 2, the yield locus exhibits corners and such values are not recommended.
Hosford yield criterion for isotropic plasticity
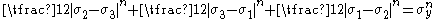
where
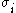, i=1,2,3 are the principal stresses, is a material-dependent exponent and 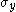is the yield stress in uniaxial tension/compression.Alternatively, the yield criterion may be written as
This expression has the form of an Lp norm
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
which is defined as
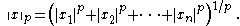
When
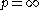, the we get the L∞ norm,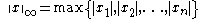. Comparing this with the Hosford criterionindicates that if n = ∞, we have
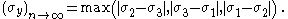
This is identical to the Tresca yield criterion.
Therefore, when n = 1 or n goes to infinity the Hosford criterion reduces to the Tresca yield criterion. When n = 2 the Hosford criterion reduces to the von Mises yield criterion.
Note that the exponent n does not need to be an integer.
Hosford yield criterion for plane stress
For the practically important situation of plane stress, the Hosford yield criterion takes the formA plot of the yield locus in plane stress for various values of the exponent
is shown in the adjacent figure.Logan-Hosford yield criterion for anisotropic plasticity
Hill yield criteria
Rodney Hill has developed several yield criteria for anisotropic plastic deformations. The earliest version was a straightforward extension of the von Mises yield criterion and had a quadratic form. This model was later generalized by allowing for an exponent m...
and has the form
where F,G,H are constants,
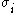are the principal stresses, and the exponent n depends on the type of crystal (bcc, fcc, hcp, etc.) and has a value much greater than 2. Accepted values of are 6 for bcc materials and 8 for fcc materials.Though the form is similar to Hill's generalized yield criterion
Hill yield criteria
Rodney Hill has developed several yield criteria for anisotropic plastic deformations. The earliest version was a straightforward extension of the von Mises yield criterion and had a quadratic form. This model was later generalized by allowing for an exponent m...
, the exponent n is independent of the R-value unlike the Hill's criterion.
Logan-Hosford criterion in plane stress
Under plane stress conditions, the Logan-Hosford criterion can be expressed aswhere
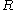is the R-value and 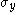is the yield stress in uniaxial tension/compression. For a derivation of this relation see Hill's yield criteria for plane stress. A plot of the yield locus for the anisotropic Hosford criterion is shown in the adjacent figure. For values of that are less than 2, the yield locus exhibits corners and such values are not recommended.See also
- Yield surfaceYield surfaceA yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...
- Yield (engineering)Yield (engineering)The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
- Plasticity (physics)Plasticity (physics)In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
- Stress (physics)Stress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...