Hull-White model
Encyclopedia
In financial mathematics, the Hull–White model is a model
of future interest rate
s. In its most generic formulation, it belongs to the class of no-arbitrage models that are able to fit today's term structure of interest rates. It is relatively straightforward to translate the mathematical description of the evolution of future interest rates onto a tree or lattice
and so interest rate derivative
s such as bermudan swaptions can be valued in the model.
The first Hull–White model was described by John C. Hull and Alan White in 1990. The model is still popular in the market today.
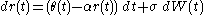
There is a degree of ambiguity amongst practitioners about exactly which parameters in the model are time-dependent or what name to apply to the model in each case.
The most commonly accepted hierarchy has
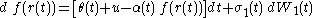
Where
has an initial value of 0 and follows the process:
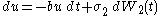
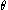has t-dependence.
Neglecting the stochastic term for a moment, notice that the change in r is negative if r is currently "large" (greater than θ(t)/α) and positive if the current value is small. That is, the stochastic process is a mean-reverting
Ornstein–Uhlenbeck process.
θ is calculated from the initial yield curve
describing the current term structure of interest rates. Typically α is left as a user input (for example it may be estimated from historical data). σ is determined via calibration
to a set of caplet
s and swaption
s readily tradeable in the market.
When
, 
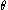and 
are constant, Itô's lemma
can be used to prove that
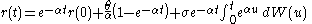
which has distribution
where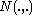
is the normal distribution.
where
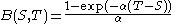
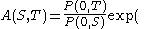
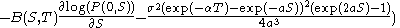
Note that their terminal distribution for P(S,T) is distributed log-normally.
the time-S bond (which corresponds to switching to the S-forward measure), we have from the fundamental theorem of arbitrage-free pricing
, the value at time 0 of a derivative which has payoff at time S.
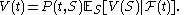
Here,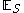
is the expectation taken with respect to the forward measure
. Moreover that standard arbitrage arguments show
that the time T forward price
for a payoff at time T given by V(T) must satisfy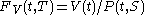 
, thus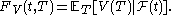
Thus it is possible to value many derivatives V dependent solely on a single bond P(S,T) analytically when working in the Hull–White model. For example in the case of a bond put
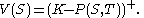
Because P(S,T) is lognormally distributed, the general calculation
used for Black-Scholes shows that
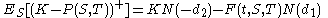
where
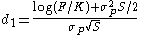
and
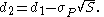
Thus today's value (with the P(0,S) multiplied back in) is:
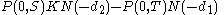
Here σP is the standard deviation of the
log-normal distribution for P(S,T). A fairly substantial amount
of algebra shows that it is related to the original parameters via
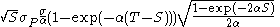
Note that this expectation was done in the S-bond measure, whereas we did not specify a measure at all for the original Hull-White process. This does not matter — the volatility is all that matters and is measure-independent.
Because interest rate caps/floors are equivalent to bond puts and calls respectively, the above analysis shows that caps and floors can be priced analytically in the Hull–White model. Jamshidian's trick
applies to Hull-White (as today's value of a swaption in HW is a monotonic function
of today's short rate). Thus knowing how to price caps is also sufficient for pricing swaptions.
s such as bermudan swaptions on a lattice or other derivatives in a multi-currency context such as Quanto Constant Maturity Swaps, as explained for example in Brigo and Mercurio (2001).
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
of future interest rate
Interest rate
An interest rate is the rate at which interest is paid by a borrower for the use of money that they borrow from a lender. For example, a small company borrows capital from a bank to buy new assets for their business, and in return the lender receives interest at a predetermined interest rate for...
s. In its most generic formulation, it belongs to the class of no-arbitrage models that are able to fit today's term structure of interest rates. It is relatively straightforward to translate the mathematical description of the evolution of future interest rates onto a tree or lattice
Lattice model (finance)
In finance, a lattice model can be used to find the fair value of a stock option; variants also exist for interest rate derivatives.The model divides time between now and the option's expiration into N discrete periods...
and so interest rate derivative
Interest rate derivative
An interest rate derivative is a derivative where the underlying asset is the right to pay or receive a notional amount of money at a given interest rate...
s such as bermudan swaptions can be valued in the model.
The first Hull–White model was described by John C. Hull and Alan White in 1990. The model is still popular in the market today.
One-factor model
The model is a short-rate model. In general, it has dynamics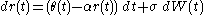There is a degree of ambiguity amongst practitioners about exactly which parameters in the model are time-dependent or what name to apply to the model in each case.
The most commonly accepted hierarchy has
- θ constant – the Vasicek modelVasicek modelIn finance, the Vasicek model is a mathematical model describing the evolution of interest rates. It is a type of "one-factor model" as it describes interest rate movements as driven by only one source of market risk...
- θ has t dependence – the Hull-White model
- θ and α also time-dependent – the extended Vasicek modelVasicek modelIn finance, the Vasicek model is a mathematical model describing the evolution of interest rates. It is a type of "one-factor model" as it describes interest rate movements as driven by only one source of market risk...
Two-factor model
The two-factor Hull–White model contains an additional disturbance term whose mean reverts to zero, and is of the form: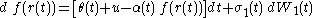Where
has an initial value of 0 and follows the process: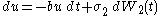Analysis of the one-factor model
For the rest of this article we assume only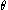 has t-dependence.Neglecting the stochastic term for a moment, notice that the change in r is negative if r is currently "large" (greater than θ(t)/α) and positive if the current value is small. That is, the stochastic process is a mean-reverting
Mean reversion
Mean reversion is a mathematical concept sometimes used for stock investing, but it can be applied to other assets. In general terms, the essence of the concept is the assumption that both a stock's high and low prices are temporary and that a stock's price will tend to move to the average price...
Ornstein–Uhlenbeck process.
θ is calculated from the initial yield curve
Yield curve
In finance, the yield curve is the relation between the interest rate and the time to maturity, known as the "term", of the debt for a given borrower in a given currency. For example, the U.S. dollar interest rates paid on U.S...
describing the current term structure of interest rates. Typically α is left as a user input (for example it may be estimated from historical data). σ is determined via calibration
Calibration
Calibration is a comparison between measurements – one of known magnitude or correctness made or set with one device and another measurement made in as similar a way as possible with a second device....
to a set of caplet
Caplet
Caplet can refer to one of the following:*A short, half-round fencing cape with a collar, worn over one sholder. A cord , ran from one end of the collar to the other, allowing it to be secured around the man's chest...
s and swaption
Swaption
A swaption is an option granting its owner the right but not the obligation to enter into an underlying swap. Although options can be traded on a variety of swaps, the term "swaption" typically refers to options on interest rate swaps....
s readily tradeable in the market.
When
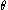, and are constant, Itô's lemmaIto's lemma
In mathematics, Itō's lemma is used in Itō stochastic calculus to find the differential of a function of a particular type of stochastic process. It is named after its discoverer, Kiyoshi Itō...
can be used to prove that
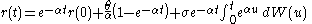
which has distribution
where
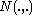is the normal distribution.Bond pricing using the Hull–White model
It turns out that the time-S value of the T-maturity discount bond has distribution (note the affine term structure here!)where
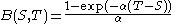
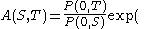
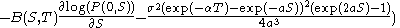
Note that their terminal distribution for P(S,T) is distributed log-normally.
Derivative pricing
By selecting as numeraireNuméraire
Numéraire is a basic standard by which values are measured. Acting as the numéraire is one of the functions of money, to serve as a unit of account: to measure the worth of different goods and services relative to one another, i.e. in same units...
the time-S bond (which corresponds to switching to the S-forward measure), we have from the fundamental theorem of arbitrage-free pricing
Fundamental theorem of arbitrage-free pricing
The fundamental theorems of arbitrage/finance provide necessary and sufficient conditions for a market to be arbitrage free and for a market to be complete. An arbitrage opportunity is a way of making money with no initial investment without any possibility of loss...
, the value at time 0 of a derivative which has payoff at time S.
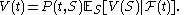
Here,
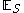is the expectation taken with respect to the forward measureForward measure
In finance, a T-forward measure is a pricing measure absolutely continuous with respect to a risk-neutral measure but rather than using the money market as numeraire, it uses a bond with maturity T...
. Moreover that standard arbitrage arguments show
that the time T forward price
for a payoff at time T given by V(T) must satisfy 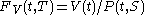, thus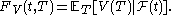Thus it is possible to value many derivatives V dependent solely on a single bond P(S,T) analytically when working in the Hull–White model. For example in the case of a bond put
Put option
A put or put option is a contract between two parties to exchange an asset, the underlying, at a specified price, the strike, by a predetermined date, the expiry or maturity...
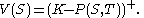
Because P(S,T) is lognormally distributed, the general calculation
used for Black-Scholes shows that
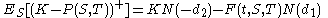
where
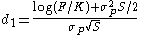
and
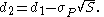
Thus today's value (with the P(0,S) multiplied back in) is:
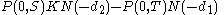
Here σP is the standard deviation of the
log-normal distribution for P(S,T). A fairly substantial amount
of algebra shows that it is related to the original parameters via
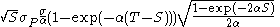
Note that this expectation was done in the S-bond measure, whereas we did not specify a measure at all for the original Hull-White process. This does not matter — the volatility is all that matters and is measure-independent.
Because interest rate caps/floors are equivalent to bond puts and calls respectively, the above analysis shows that caps and floors can be priced analytically in the Hull–White model. Jamshidian's trick
Jamshidian's trick
Jamshidian's trick is a technique for one-factor asset price models, which re-expresses an option on a portfolio of assets as a portfolio of options...
applies to Hull-White (as today's value of a swaption in HW is a monotonic function
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
of today's short rate). Thus knowing how to price caps is also sufficient for pricing swaptions.
Trees and lattices
However, valuing vanilla instruments such as caps and swaptions is useful primarily for calibration. The real use of the model is to value somewhat more exotic optionExotic option
In finance, an exotic option is a derivative which has features making it more complex than commonly traded products . These products are usually traded over-the-counter , or are embedded in structured notes....
s such as bermudan swaptions on a lattice or other derivatives in a multi-currency context such as Quanto Constant Maturity Swaps, as explained for example in Brigo and Mercurio (2001).
See also
- Ho-Lee modelHo-Lee modelIn financial mathematics, the Ho–Lee model is a short rate model used in the pricing of bond options, swaptions and other interest rate derivatives, and in modeling future interest rates. It is the simplest model that can be calibrated to market data, by implying the form of \theta_t from market...
- Vasicek modelVasicek modelIn finance, the Vasicek model is a mathematical model describing the evolution of interest rates. It is a type of "one-factor model" as it describes interest rate movements as driven by only one source of market risk...
- Cox–Ingersoll–Ross model
- Black-Karasinski model