Vasicek model
Encyclopedia
In finance
, the Vasicek model is a mathematical model
describing the evolution of interest rate
s. It is a type of "one-factor model" (more precisely, one factor short rate model
) as it describes interest rate movements as driven by only one source of market risk
. The model can be used in the valuation of interest rate derivative
s, and has also been adapted for credit markets, although its use in the credit market is in principle wrong, implying negative probabilities (see for example Brigo and Mercurio (2006), Section 21.1.1). It was introduced in 1977 by Oldrich Vasicek
and can be also seen as an stochastic investment model
.
:
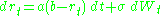
where Wt is a Wiener process
under the risk neutral framework modelling the random market risk factor, in that it models the continuous inflow of randomness into the system. The standard deviation
parameter,
, determines the volatility
of the interest rate and in a way characterizes the amplitude of the instantaneous randomness inflow. The typical parameters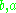
and 
, together with the initial condition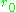 
, completely characterize the dynamics, and can be quickly characterized as follows, assuming 
to be non-negative:
The following derived quantity is also of interest,
and 
tend to oppose each other: increasing 
increases the amount of randomness entering the system, but at the same time increasing 
amounts to increasing the speed at which the system will stabilize statistically around the long term mean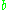 
with a corridor of variance determined also by 
. This is clear when looking at the long term variance,
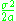
which increases with
but decreases with 
.
This model is an Ornstein–Uhlenbeck stochastic process.
prices for instance, interest rates cannot rise indefinitely. This is because at very high levels they would hamper economic activity, prompting a decrease in interest rates. Similarly, interest rates can not decrease below 0. As a result, interest rates move in a limited range, showing a tendency to revert to a long run value.
The drift factor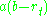
represents the expected instantaneous change in the interest rate at time t. The parameter b represents the long run equilibrium
value towards which the interest rate reverts. Indeed, in the absence of shocks (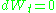
), the interest remains constant when rt = b. The parameter a, governing the speed of adjustment, needs to be positive to ensure stability
around the long term value. For example, when rt is below b, the drift term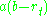
becomes positive for positive a, generating a tendency for the interest rate to move upwards (toward equilibrium).
The main disadvantage is that, under Vasicek's model, it is theoretically possible for the interest rate to become negative, an undesirable feature. This shortcoming was fixed in the Cox–Ingersoll–Ross model, exponential Vasicek model, Black–Derman–Toy model and Black Karasinsky, among many others. The Vasicek model was further extended in the Hull–White model. The Vasicek model is also a canonical example of the affine term structure model, along with the Cox–Ingersoll–Ross model.
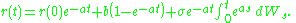
Using similar techniques as applied to the Ornstein–Uhlenbeck stochastic process this has mean
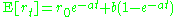
and variance
Consequently, we have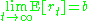
and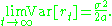
Mathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
, the Vasicek model is a mathematical model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
describing the evolution of interest rate
Interest rate
An interest rate is the rate at which interest is paid by a borrower for the use of money that they borrow from a lender. For example, a small company borrows capital from a bank to buy new assets for their business, and in return the lender receives interest at a predetermined interest rate for...
s. It is a type of "one-factor model" (more precisely, one factor short rate model
Short rate model
In the context of interest rate derivatives, a short-rate model is a mathematical model that describes the future evolution of interest rates by describing the future evolution of the short rate, usually written r_t \,.-The short rate:...
) as it describes interest rate movements as driven by only one source of market risk
Market risk
Market risk is the risk that the value of a portfolio, either an investment portfolio or a trading portfolio, will decrease due to the change in value of the market risk factors. The four standard market risk factors are stock prices, interest rates, foreign exchange rates, and commodity prices...
. The model can be used in the valuation of interest rate derivative
Interest rate derivative
An interest rate derivative is a derivative where the underlying asset is the right to pay or receive a notional amount of money at a given interest rate...
s, and has also been adapted for credit markets, although its use in the credit market is in principle wrong, implying negative probabilities (see for example Brigo and Mercurio (2006), Section 21.1.1). It was introduced in 1977 by Oldrich Vasicek
Oldrich Vasicek
Oldrich Alfons Vasicek a Czech mathematician, received his master's degree in math from the Czech Technical University, 1964, and a doctorate in probability theory from Charles University four years later....
and can be also seen as an stochastic investment model
Stochastic investment model
A stochastic investment model tries to forecast how returns and prices on different assets or asset classes, vary over time. Stochastic models are not applied for making point estimation rather interval estimation and they use different stochastic processes. Investment models can be classified...
.
Details
The model specifies that the instantaneous interest rate follows the stochastic differential equationStochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
:
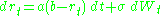
where Wt is a Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
under the risk neutral framework modelling the random market risk factor, in that it models the continuous inflow of randomness into the system. The standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
parameter,
, determines the volatilityVolatility (finance)
In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
of the interest rate and in a way characterizes the amplitude of the instantaneous randomness inflow. The typical parameters
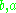and , together with the initial condition 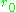, completely characterize the dynamics, and can be quickly characterized as follows, assuming to be non-negative:-
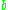: "long term mean level". All future trajectories of 
will evolve around a mean level b in the long run; -
: "speed of reversion". 
characterizes the velocity at which such trajectories will regroup around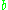 
in time; -
: "instantaneous volatility", measures instant by instant the amplitude of randomness entering the system. Higher 
implies more randomness
The following derived quantity is also of interest,
-
: "long term variance". All future trajectories of 
will regroup around the long term mean with such variance after a long time.
and tend to oppose each other: increasing increases the amount of randomness entering the system, but at the same time increasing amounts to increasing the speed at which the system will stabilize statistically around the long term mean 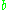with a corridor of variance determined also by . This is clear when looking at the long term variance,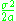which increases with
but decreases with .This model is an Ornstein–Uhlenbeck stochastic process.
Discussion
Vasicek's model was the first one to capture mean reversion, an essential characteristic of the interest rate that sets it apart from other financial prices. Thus, as opposed to stockCommon stock
Common stock is a form of corporate equity ownership, a type of security. It is called "common" to distinguish it from preferred stock. In the event of bankruptcy, common stock investors receive their funds after preferred stock holders, bondholders, creditors, etc...
prices for instance, interest rates cannot rise indefinitely. This is because at very high levels they would hamper economic activity, prompting a decrease in interest rates. Similarly, interest rates can not decrease below 0. As a result, interest rates move in a limited range, showing a tendency to revert to a long run value.
The drift factor
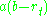represents the expected instantaneous change in the interest rate at time t. The parameter b represents the long run equilibriumSteady state
A system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero:...
value towards which the interest rate reverts. Indeed, in the absence of shocks (
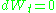), the interest remains constant when rt = b. The parameter a, governing the speed of adjustment, needs to be positive to ensure stabilityStability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
around the long term value. For example, when rt is below b, the drift term
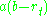becomes positive for positive a, generating a tendency for the interest rate to move upwards (toward equilibrium).The main disadvantage is that, under Vasicek's model, it is theoretically possible for the interest rate to become negative, an undesirable feature. This shortcoming was fixed in the Cox–Ingersoll–Ross model, exponential Vasicek model, Black–Derman–Toy model and Black Karasinsky, among many others. The Vasicek model was further extended in the Hull–White model. The Vasicek model is also a canonical example of the affine term structure model, along with the Cox–Ingersoll–Ross model.
Asymptotic mean and variance
We solve the stochastic differential equation to obtain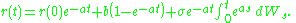Using similar techniques as applied to the Ornstein–Uhlenbeck stochastic process this has mean
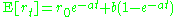
and variance
Consequently, we have
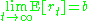
and
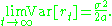
External links
- An Equilibrium Characterisation of the Term Structure, Oldrich Vasicek,(1977). Journal of Financial Economics 5: 177–188
- The Vasicek Model, Bjørn Eraker, Wisconsin School of BusinessWisconsin School of BusinessThe Wisconsin School of Business is the business school of University of Wisconsin–Madison, located in Grainger Hall. Founded in 1900, it has more than 35,000 alumni. The undergraduate program prepares students for business careers, while its Master of Business Administration program is based on...
- Yield Curve Estimation and Prediction with the Vasicek Model, D. Bayazit, Middle East Technical UniversityMiddle East Technical UniversityMiddle East Technical University is a public technical university located in Ankara, Turkey...