Hungarian algorithm
Encyclopedia
The Hungarian method is a combinatorial optimization
algorithm
which solves the assignment problem
in polynomial time and which anticipated later primal-dual methods. It was developed and published by Harold Kuhn in 1955, who gave the name "Hungarian method" because the algorithm was largely based on the earlier works of two Hungarian
mathematicians: Dénes Kőnig
and Jenő Egerváry
.
James Munkres
reviewed the algorithm in 1957 and observed that it is (strongly) polynomial. Since then the algorithm has been known also as Kuhn–Munkres algorithm or Munkres assignment algorithm. The time complexity of the original algorithm was
, however Edmonds
and Karp
, and independently Tomizawa noticed that it can be modified to achieve an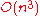
running time. Ford
and Fulkerson
extended the method to general transportation problems. In 2006, it was discovered that Carl Gustav Jacobi had
solved the assignment problem in the 19th century, and published posthumously in 1890 in Latin.
You need to have one of them clean the bathroom, another sweep the floors & the third wash the windows.
What’s the best (minimum-cost) way to assign the jobs?
First we need a matrix
of the costs of the workers doing the jobs.
Then the Hungarian algorithm, when applied to the above table would give us the minimum cost it can be done with: Jim cleans the bathroom, Steve sweeps the floors and Alan washes the windows.
, where the element in the i-th row and j-th column represents the cost of assigning the j-th job to the i-th worker. We have to find an assignment of the jobs to the workers that has minimum cost. If the goal is to find the assignment that yields the maximum cost, the problem can be altered to fit the setting by replacing each cost with the maximum cost subtracted by the cost.
The algorithm is easier to describe if we formulate the problem using a bipartite graph. We have a complete bipartite graph
G=(S, T; E) with n worker vertices (S) and n job vertices (T), and each edge has a nonnegative cost c(i,j). We want to find a perfect matching with minimum cost.
Let us call a function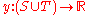
a potential if 
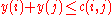for each 
. The value of potential y is 
. It can be seen that the cost of each perfect matching is at least the value of each potential. The Hungarian method finds a perfect matching and a potential with equal cost/value which proves the optimality of both. In fact it finds a perfect matching of tight edges: an edge ij is called tight for a potential y if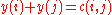 
. Let us denote the subgraph of tight edges by 
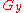. The cost of a perfect matching in 
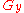(if there is one) equals the value of y.
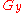(denoted by 
) which has the property that the edges oriented from T to S form a matching M. Initially, y is 0 everywhere, and all edges are oriented from S to T (so M is empty). In each step, either we modify y so that its value increases, or modify the orientation to obtain a matching with more edges. We maintain the invariant that all the edges of M are tight. We are done if M is a perfect matching.
In a general step, let
and 
be the vertices not covered by M (so
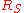consists of the vertices in S with no incoming edge and 
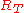consists of the vertices in T with no outgoing edge). Let 
be the set of vertices reachable in 
from 
by a directed path only following edges that are tight. This can be computed by breadth-first search
.
If
is nonempty, then reverse the orientation of a directed path in 
from 
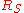to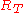 
. Thus the size of the corresponding matching increases by 1.
If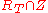
is empty, then let 
. 
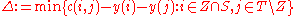is positive because there are no tight edges between 
and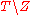 
. Increase y by 
on the vertices of 
and decrease y by 
on the vertices of 
. The resulting y is still a potential. The graph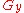 
changes, but it still contains M. We orient the new edges from S to T. By the definition of 
the set Z of vertices reachable from 
increases (note that the number of tight edges does not necessarily increase).
We repeat these steps until M is a perfect matching, in which case it gives a minimum cost assignment. The running time of this version of the method is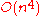
: M is augmented n times, and in a phase where M is unchanged, there are at most n potential changes (since Z increases every time). The time needed for a potential change is 
.
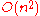workers and tasks, and an n×n matrix containing the cost of assigning each worker to a task, find the cost minimizing assignment.
First the problem is written in the form of a matrix as given below
where a, b, c and d are the workers who have to perform tasks 1, 2, 3 and 4. a1, a2, a3, a4 denote the penalties incurred when worker "a" does task 1, 2, 3, 4 respectively. The same holds true for the other symbols as well. The matrix is square, so each worker can perform only one task.
Step 1
Then we perform row operations on the matrix. To do this, the lowest of all ai (i belonging to 1-4) is taken and is subtracted from each element in that row. This will lead to at least one zero in that row (We get multiple zeros when there are two equal elements which also happen to be the lowest in that row). This procedure is repeated for all rows. We now have a matrix with at least one zero per row. Now we try to assign tasks to agents such that each agent is doing only one task and the penalty incurred in each case is zero. This is illustrated below.
The zeros that are indicated as 0' are the assigned tasks.
Step 2
Sometimes it may turn out that the matrix at this stage cannot be used for assigning, as is the case in for the matrix below.
In the above case, no assignment can be made. Note that task 1 is done efficiently by both agent a and c. Both can't be assigned the same task. Also note that no one does task 3 efficiently.
To overcome this, we repeat the above procedure for all columns (i.e. the minimum element in each column is subtracted from all the elements in that column) and then check if an assignment is possible.
Step 3
In most situations this will give the result, but if it is still not possible to assign then the procedure described below must be followed.
Initially assign as many tasks as possible then do the following (assign tasks in rows 2, 3 and 4)
Mark all rows having no assignments (row 1). Then mark all columns having zeros in that row(s) (column 1). Then mark all rows having assignments in the given column (row 3). Repeat this till a closed loop is obtained.
Now draw lines through all marked columns and unmarked rows.
The aforementioned detailed description is just one way to draw the minimum number of lines to cover all the 0's. Other methods work as well.
Step 4
From the elements that are left, find the lowest value. Subtract this from every unmarked element and add it to every element covered by two lines.
Repeat the procedure (steps 1–4) till an assignment is possible; this is when the minimum number of lines used to cover all the 0's is equal to the max(number of people, number of assignments), assuming dummy variables (usually the max cost) are used to fill in when the number of people is greater than the number of assignments.
Basically you find the second minimum cost among the two rows. The procedure is repeated until you are able to distinguish among the workers in terms of least cost.
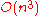time constraint.)
Combinatorial optimization
In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
which solves the assignment problem
Assignment problem
The assignment problem is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics...
in polynomial time and which anticipated later primal-dual methods. It was developed and published by Harold Kuhn in 1955, who gave the name "Hungarian method" because the algorithm was largely based on the earlier works of two Hungarian
Hungary
Hungary , officially the Republic of Hungary , is a landlocked country in Central Europe. It is situated in the Carpathian Basin and is bordered by Slovakia to the north, Ukraine and Romania to the east, Serbia and Croatia to the south, Slovenia to the southwest and Austria to the west. The...
mathematicians: Dénes Kőnig
Dénes König
Dénes Kőnig was a Jewish Hungarian mathematician who worked in and wrote the first textbook on the field of graph theory....
and Jenő Egerváry
Jenő Egerváry
Jenő Egerváry was a Hungarian mathematician.-Biography:Egerváry was born in Debrecen in 1891. In 1914, he received his doctorate at the Pázmány Péter University in Budapest, where he studied under the supervision of Lipót Fejér...
.
James Munkres
James Munkres
James Raymond Munkres is a Professor Emeritus of mathematics at MIT and the author of several texts in the area of topology, including Topology , Analysis on Manifolds, Elements of Algebraic Topology, and Elementary Differential Topology...
reviewed the algorithm in 1957 and observed that it is (strongly) polynomial. Since then the algorithm has been known also as Kuhn–Munkres algorithm or Munkres assignment algorithm. The time complexity of the original algorithm was
, however EdmondsJack Edmonds
Jack R. Edmonds is a mathematician, regarded as one of the most important contributors to the field of combinatorial optimization...
and Karp
Richard Karp
Richard Manning Karp is a computer scientist and computational theorist at the University of California, Berkeley, notable for research in the theory of algorithms, for which he received a Turing Award in 1985, The Benjamin Franklin Medal in Computer and Cognitive Science in 2004, and the Kyoto...
, and independently Tomizawa noticed that it can be modified to achieve an
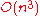running time. FordL. R. Ford, Jr.
Lester Randolph Ford, Jr. is an American mathematician specializing in network flow problems. He is the son of mathematician Lester R. Ford, Sr..Ford's paper with D. R...
and Fulkerson
D. R. Fulkerson
Delbert Ray Fulkerson was a mathematician who co-developed the Ford-Fulkerson algorithm, one of the most well-known algorithms to solve the maximum flow problem in networks....
extended the method to general transportation problems. In 2006, it was discovered that Carl Gustav Jacobi had
solved the assignment problem in the 19th century, and published posthumously in 1890 in Latin.
Layman’s explanation
Say you have three workers: Jim, Steve and Alan.You need to have one of them clean the bathroom, another sweep the floors & the third wash the windows.
What’s the best (minimum-cost) way to assign the jobs?
First we need a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
of the costs of the workers doing the jobs.
| Clean bathroom | Sweep floors | Wash windows | |
|---|---|---|---|
| Jim | $1 | $2 | $3 |
| Steve | $3 | $3 | $3 |
| Alan | $3 | $3 | $2 |
Then the Hungarian algorithm, when applied to the above table would give us the minimum cost it can be done with: Jim cleans the bathroom, Steve sweeps the floors and Alan washes the windows.
Setting
We are given a nonnegative n×n matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, where the element in the i-th row and j-th column represents the cost of assigning the j-th job to the i-th worker. We have to find an assignment of the jobs to the workers that has minimum cost. If the goal is to find the assignment that yields the maximum cost, the problem can be altered to fit the setting by replacing each cost with the maximum cost subtracted by the cost.
The algorithm is easier to describe if we formulate the problem using a bipartite graph. We have a complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
G=(S, T; E) with n worker vertices (S) and n job vertices (T), and each edge has a nonnegative cost c(i,j). We want to find a perfect matching with minimum cost.
Let us call a function
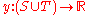a potential if 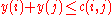for each . The value of potential y is . It can be seen that the cost of each perfect matching is at least the value of each potential. The Hungarian method finds a perfect matching and a potential with equal cost/value which proves the optimality of both. In fact it finds a perfect matching of tight edges: an edge ij is called tight for a potential y if 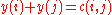. Let us denote the subgraph of tight edges by 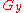. The cost of a perfect matching in 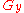(if there is one) equals the value of y.The algorithm in terms of bipartite graphs
During the algorithm we maintain a potential y and an orientation of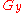 (denoted by ) which has the property that the edges oriented from T to S form a matching M. Initially, y is 0 everywhere, and all edges are oriented from S to T (so M is empty). In each step, either we modify y so that its value increases, or modify the orientation to obtain a matching with more edges. We maintain the invariant that all the edges of M are tight. We are done if M is a perfect matching.In a general step, let
and be the vertices not covered by M (so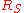 consists of the vertices in S with no incoming edge and 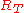consists of the vertices in T with no outgoing edge). Let be the set of vertices reachable in from by a directed path only following edges that are tight. This can be computed by breadth-first searchBreadth-first search
In graph theory, breadth-first search is a graph search algorithm that begins at the root node and explores all the neighboring nodes...
.
If
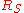is nonempty, then reverse the orientation of a directed path in from to 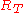. Thus the size of the corresponding matching increases by 1.If
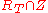is empty, then let 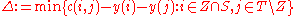. is positive because there are no tight edges between and 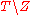. Increase y by on the vertices of and decrease y by on the vertices of . The resulting y is still a potential. The graph 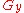changes, but it still contains M. We orient the new edges from S to T. By the definition of the set Z of vertices reachable from increases (note that the number of tight edges does not necessarily increase).We repeat these steps until M is a perfect matching, in which case it gives a minimum cost assignment. The running time of this version of the method is
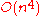: M is augmented n times, and in a phase where M is unchanged, there are at most n potential changes (since Z increases every time). The time needed for a potential change is 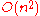.Matrix interpretation
Given workers and tasks, and an n×n matrix containing the cost of assigning each worker to a task, find the cost minimizing assignment.First the problem is written in the form of a matrix as given below
where a, b, c and d are the workers who have to perform tasks 1, 2, 3 and 4. a1, a2, a3, a4 denote the penalties incurred when worker "a" does task 1, 2, 3, 4 respectively. The same holds true for the other symbols as well. The matrix is square, so each worker can perform only one task.
Step 1
Then we perform row operations on the matrix. To do this, the lowest of all ai (i belonging to 1-4) is taken and is subtracted from each element in that row. This will lead to at least one zero in that row (We get multiple zeros when there are two equal elements which also happen to be the lowest in that row). This procedure is repeated for all rows. We now have a matrix with at least one zero per row. Now we try to assign tasks to agents such that each agent is doing only one task and the penalty incurred in each case is zero. This is illustrated below.
| 0 | a2' | 0' | a4' |
| b1' | b2' | b3' | 0' |
| 0' | c2' | c3' | c4' |
| d1' | 0' | d3' | d4' |
The zeros that are indicated as 0' are the assigned tasks.
Step 2
Sometimes it may turn out that the matrix at this stage cannot be used for assigning, as is the case in for the matrix below.
| 0 | a2' | a3' | a4' |
| b1' | b2' | b3' | 0 |
| 0 | c2' | c3' | c4' |
| d1' | 0 | d3' | d4' |
In the above case, no assignment can be made. Note that task 1 is done efficiently by both agent a and c. Both can't be assigned the same task. Also note that no one does task 3 efficiently.
To overcome this, we repeat the above procedure for all columns (i.e. the minimum element in each column is subtracted from all the elements in that column) and then check if an assignment is possible.
Step 3
In most situations this will give the result, but if it is still not possible to assign then the procedure described below must be followed.
Initially assign as many tasks as possible then do the following (assign tasks in rows 2, 3 and 4)
| 0 | a2' | a3' | a4' |
| b1' | b2' | b3' | 0' |
| 0' | c2' | c3' | c4' |
| d1' | 0' | d3' | d4' |
Mark all rows having no assignments (row 1). Then mark all columns having zeros in that row(s) (column 1). Then mark all rows having assignments in the given column (row 3). Repeat this till a closed loop is obtained.
| × | ||||
| 0 | a2' | a3' | a4' | × |
| b1' | b2' | b3' | 0' | |
| 0' | c2' | c3' | c4' | × |
| d1' | 0' | d3' | d4' |
Now draw lines through all marked columns and unmarked rows.
| × | ||||
| 0 | a2' | a3' | a4' | × |
| b1' | b2' | b3' | 0' | |
| 0' | c2' | c3' | c4' | × |
| d1' | 0' | d3' | d4' |
The aforementioned detailed description is just one way to draw the minimum number of lines to cover all the 0's. Other methods work as well.
Step 4
From the elements that are left, find the lowest value. Subtract this from every unmarked element and add it to every element covered by two lines.
Repeat the procedure (steps 1–4) till an assignment is possible; this is when the minimum number of lines used to cover all the 0's is equal to the max(number of people, number of assignments), assuming dummy variables (usually the max cost) are used to fill in when the number of people is greater than the number of assignments.
Basically you find the second minimum cost among the two rows. The procedure is repeated until you are able to distinguish among the workers in terms of least cost.
External links
- Mordecai J. Golin, Bipartite Matching and the Hungarian Method, Course Notes, Hong Kong University of Science and TechnologyHong Kong University of Science and TechnologyThe Hong Kong University of Science and Technology is a public university located in Hong Kong. Established in 1991 under Hong Kong Law Chapter 1141 , it is one of the nine universities in Hong Kong.Professor Tony F. Chan is the president of HKUST...
. - R. A. Pilgrim, Munkres' Assignment Algorithm. Modified for Rectangular Matrices, Course notes, Murray State UniversityMurray State UniversityMurray State University, located in the city of Murray, Kentucky, is a four-year public university with approximately 10,400 students. The school is Kentucky’s only public university to be listed in the U.S.News & World Report regional university top tier for the past 20 consecutive years...
. - Mike Dawes, The Optimal Assignment Problem, Course notes, University of Western OntarioUniversity of Western OntarioThe University of Western Ontario is a public research university located in London, Ontario, Canada. The university's main campus covers of land, with the Thames River cutting through the eastern portion of the main campus. Western administers its programs through 12 different faculties and...
. - On Kuhn's Hungarian Method – A tribute from Hungary, András FrankAndrás FrankAndrás Frank is a Hungarian mathematician, working in combinatorics, especially in graph theory, and combinatorial optimisation...
, Egervary Research Group, Pazmany P. setany 1/C, H1117, Budapest, Hungary.
Implementations
(Note that not all of these satisfy the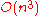 time constraint.)
- Java implementation
- Python implementation (see also here)
- Ruby implementation with unit tests
- C# implementation
- Online interactive implementation Please note that this implements a variant of the algorithm as described above.
- Graphical implementation with options (Java appletJava appletA Java applet is an applet delivered to users in the form of Java bytecode. Java applets can run in a Web browser using a Java Virtual Machine , or in Sun's AppletViewer, a stand-alone tool for testing applets...
) - Serial and parallel implementations.
- Implementation in Matlab and C
- Perl implementation
- Lisp implementation
- C++ (STL) implementation (multi-functional bipartite graph version)
- C++ implementation
- Another C++ implementation with unit tests
- Another Java implementation with JUnit tests (Apache 2.0)
- Matlab implementation
- https://launchpad.net/lib-bipartite-match