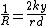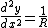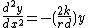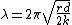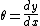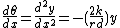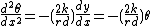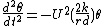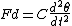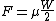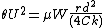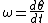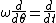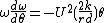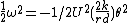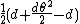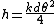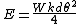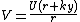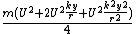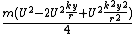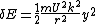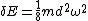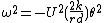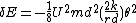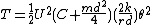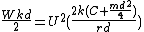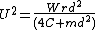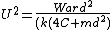Hunting oscillation

Encyclopedia

Hunting oscillation is an oscillation

Oscillation

Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...

, usually unwanted, about an equilibrium

Mechanical equilibrium

A standard definition of static equilibrium is:This is a strict definition, and often the term "static equilibrium" is used in a more relaxed manner interchangeably with "mechanical equilibrium", as defined next....

. The expression came into use in the 19th century and describes how a systems 'hunts

Hunting

Hunting is the practice of pursuing any living thing, usually wildlife, for food, recreation, or trade. In present-day use, the term refers to lawful hunting, as distinguished from poaching, which is the killing, trapping or capture of the hunted species contrary to applicable law...

' for equilibrium. The expression is used to describe phenomena in such diverse fields as electronics, aviation, biology, and railway engineering.

Railway wheelsets

A classical hunting oscillation is a swaying motion of a railway vehicle caused by the coning action on which the directional stability

Directional stability

Directional stability is stability of a moving body or vehicle about an axis which is perpendicular to its direction of motion. Stability of a vehicle concerns itself with the tendency of a vehicle to return to its original direction in relation to the oncoming medium when disturbed away from...

of an adhesion railway depends. It arises from the interaction of adhesion

Adhesion

Adhesion is any attraction process between dissimilar molecular species that can potentially bring them in close contact. By contrast, cohesion takes place between similar molecules....

forces and inertial forces. At low speed, adhesion dominates but, as the speed increases, the adhesion forces and inertial forces become comparable in magnitude and the oscillation

Oscillation

begins at a critical speed. Above this speed, the motion can be violent, damaging track and wheels and potentially causing derailment

Derailment

A derailment is an accident on a railway or tramway in which a rail vehicle, or part or all of a train, leaves the tracks on which it is travelling, with consequent damage and in many cases injury and/or death....

. The problem does not occur on systems with a differential because the action depends on both wheels of a wheelset rotating at the same angular rate, although differentials tend to be rare, and conventional trains have their wheels fixed to the axles in pairs instead.

The problem was first noticed towards the end of the 19th Century, when train speeds became high enough to encounter it. This behaviour limited trains to operate at speeds of about 140 mph or less and led to a number of research projects in the 1960s using hovertrain

Hovertrain

A hovertrain is a type of high-speed train that replaces conventional steel wheels with hovercraft lift pads, and the conventional railway bed with a paved road-like surface, known as the "track" or "guideway"...

s and maglev systems to avoid it and reach higher speeds. But after empirical studies by the British Rail Research Division

British Rail Research Division

The British Rail Research Division came into being in 1964 directly under the control of the British Railways Board, moving into purpose-built premises at the Railway Technical Centre in Derby. The intention was to improve railway reliability and efficiency, while reducing costs and improving revenue...

in the 1960s, remedial measures, particularly in the design of suspension

Suspension (vehicle)

Suspension is the term given to the system of springs, shock absorbers and linkages that connects a vehicle to its wheels. Suspension systems serve a dual purpose — contributing to the car's roadholding/handling and braking for good active safety and driving pleasure, and keeping vehicle occupants...

systems, have been introduced permitting speeds exceeding 180 mph (290 km/h). Today, most high-speed trains use steel wheels, as a result of this research.

Kinematic analysis

Deeper understanding of the phenomenon inevitably requires a mathematical analysis of the vehicle dynamics

Dynamics (mechanics)

In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...

, which may not be accessible to all readers.

A kinematic description deals with the geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

of motion, without reference to the force

Force

In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...

s causing it, so the analysis begins with a description of the geometry of a wheel set running on a straight track. Since Newton's Second Law relates forces to acceleration

Acceleration

In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...

s of bodies, the forces acting may then be derived from the kinematics by calculating the accelerations of the components.

The train stays on the track by virtue of the conical shape of the wheel treads

Tire

A tire or tyre is a ring-shaped covering that fits around a wheel rim to protect it and enable better vehicle performance by providing a flexible cushion that absorbs shock while keeping the wheel in close contact with the ground...

. If a wheelset is displaced to one side by an amount "y", the radius of the tread in contact with the rail on one side is reduced, whilst on the other side it is increased. The angular velocity

Angular velocity

In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...

is the same for both wheels (they are coupled via a rigid

Stiffness

Stiffness is the resistance of an elastic body to deformation by an applied force along a given degree of freedom when a set of loading points and boundary conditions are prescribed on the elastic body.-Calculations:...

axle

Axle

An axle is a central shaft for a rotating wheel or gear. On wheeled vehicles, the axle may be fixed to the wheels, rotating with them, or fixed to its surroundings, with the wheels rotating around the axle. In the former case, bearings or bushings are provided at the mounting points where the axle...

), so the larger diameter

Diameter

In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...

tread speeds up, whilst the smaller slows down. The wheel set steers around a centre of curvature defined by the intersection of the generator of a cone passing through the points of contact with the wheels on the rails and the axis of the wheel set. Applying similar triangles, we have for the turn radius:

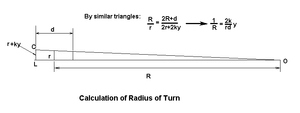
where d is the track gauge

Rail gauge

Track gauge or rail gauge is the distance between the inner sides of the heads of the two load bearing rails that make up a single railway line. Sixty percent of the world's railways use a standard gauge of . Wider gauges are called broad gauge; smaller gauges, narrow gauge. Break-of-gauge refers...

, r the wheel radius when running straight and k is the tread taper.

The path of the wheel set relative to the straight track is defined by a function y(x) where x is the progress along the track. Provided the direction of motion remains more or less parallel

Parallel (geometry)

Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...

to the rails, the curvature

Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...

of the path may be related to the second derivative

Derivative

In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...

of y with respect to distance along the track:

It follows that the trajectory

Trajectory

A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...

along the track is governed by the equation:

This is a simple harmonic motion

Simple harmonic motion

Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....

having wavelength:

This kinematic analysis implies that trains sway from side to side all the time. In fact, this oscillation is damped

Damping

In physics, damping is any effect that tends to reduce the amplitude of oscillations in an oscillatory system, particularly the harmonic oscillator.In mechanics, friction is one such damping effect...

out below a critical speed and the ride is correspondingly more comfortable. The kinematic result ignores the forces causing the motion. These are difficult to quantify simply, as they arise from the elastic distortion of the wheel and rail at the regions of contact. These are the subject of frictional contact mechanics

Frictional contact mechanics

Contact mechanics is the study of the deformation of solids that touch each other at one or more points. This can be divided into compressive and adhesive forces in the direction perpendicular to the interface, and frictional forces in the tangential direction...

; an early presentation that includes these effects in hunting motion analysis was presented by Carter. See Knothe for a historical overview.

If the motion is substantially parallel with the rails, the angular displacement of the wheel set (

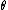) is given by:

Hence:

The angular deflection also follows a simple harmonic motion, which lags behind the side to side motion by a quarter of a cycle. In many systems which are characterised by harmonic motion involving two different states (in this case the axle yaw deflection and the lateral displacement), the quarter cycle lag between the two motions endows the system with the ability to extract energy from the forward motion. This effect is observed in 'flutter' of aircraft wings and 'shimmy

Speed wobble

Wobble, shimmy, tank-slapper, speed wobble, and even death wobble are all words and phrases used to describe a quick oscillation of primarily just the steerable wheel of a vehicle. Initially, the rest of the vehicle remains mostly unaffected, until translated into a vehicle yaw oscillation of...

' of road vehicles, as well as hunting of railway vehicles. The kinematic solution derived above describes the motion at the critical speed.

In practice, below the critical speed, the lag between the two motions is less than a quarter cycle so that the motion is damped out but, above the critical speed, the lag is greater than a quarter cycle so that the motion is amplified.

In order to estimate the inertia

Inertia

Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...

l forces, it is necessary to express the distance derivatives as time derivative

Derivative

s. This is done using the speed of the vehicle U, which is assumed constant:

The angular acceleration of the axle in yaw is:

The inertial moment (ignoring gyroscopic effects) is:

where F is the force acting along the rails and C is the moment of inertia

Moment of inertia

In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...

of the wheel set.

the maximum friction

Friction

Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...

al force between the wheel and rail is given by:

where W is the axle load and

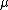is the coefficient of friction. Gross slipping will occur at a combination of speed and axle deflection given by:

this expression yields a significant overestimate of the critical speed, but it does illustrate the physical reason why hunting occurs, i.e. the inertial forces become comparable with the adhesion forces above a certain speed. Limiting friction is a poor representation of the adhesion force in this case.

The actual adhesion forces arise from the distortion of the tread and rail in the region of contact. There is no gross slippage, just elastic distortion and some local slipping. During normal operation these forces are well within the limiting friction constraint. A complete analysis takes these forces into account, using rolling contact mechanics

Frictional contact mechanics

theories.

Energy balance

In order to get an estimate of the critical speed, we use the fact that the condition for which this kinematic solution is valid corresponds to the case where there is no net energy

Energy

In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...

exchange with the surroundings, so by considering the kinetic

Kinetic energy

The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...

and potential energy

Potential energy

In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...

of the system, we should be able to derive the critical speed.
Let:

Using the operator:

the angular acceleration equation may be expressed in terms of the angular velocity in yaw :

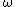
integrating:

so the kinetic energy due to rotation is:

When the axle yaws, the points of contact move outwards on the treads so that the height of the axle is lowered. The distance between the support points increases to:

(to second order of small quantities).
the displacement of the support point out from the centres of the treads is:

the axle load falls by

The work done by lowering the axle load is therefore:

This is energy lost from the system, so in order for the motion to continue, an equal amount of energy must be extracted from the forward motion of the wheelset.

The outer wheel velocity is given by:

The kinetic energy is:

for the inner wheel it is

where m is the mass

Mass

Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...

of both wheels.

The increase in kinetic energy

Kinetic energy

is:

The motion will continue at constant amplitude as long as the energy

Energy

In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...

extracted from the forward motion, and manifesting itself as increased kinetic energy of the wheel set at zero yaw, is equal to the potential energy

Potential energy

In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...

lost by the lowering of the axle load at maximum yaw.

Now, from the kinematics:

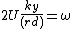
but

The translational kinetic energy is

The total kinetic energy is:

The critical speed is found from the energy balance:

Hence the critical speed is given by

This is independent of the wheel taper, but depends on the ratio of the axle load

Structural load

Structural loads or actions are forces, deformations or accelerations applied to a structure or its components.Loads cause stresses, deformations and displacements in structures. Assessment of their effects is carried out by the methods of structural analysis...

to wheel set mass. If the treads were truly conical in shape, the critical speed would be independent of the taper. In practice, wear on the wheel causes the taper to vary across the tread width, so that the value of taper used to determine the potential energy is different from that used to calculate the kinetic energy. Denoting the former as a, the critical speed becomes:

where a is now a shape factor determined by the wheel wear

Wear

In materials science, wear is erosion or sideways displacement of material from its "derivative" and original position on a solid surface performed by the action of another surface....

. This result is derived in from an analysis of the system dynamics using standard control engineering

Control engineering

Control engineering or Control systems engineering is the engineering discipline that applies control theory to design systems with predictable behaviors...

methods.

Concluding comments

The motion of a wheel set is much more complicated than this analysis would indicate. There are additional restraining forces applied by the vehicle suspension and, at high speed, the wheel set will generate additional gyroscopic torques, which will modify the estimate of the critical speed. A real railway vehicle has many more degrees of freedom and, consequently, may have more than one critical speed; it is by no means certain that the lowest is dictated by the wheelset motion.

However, the analysis is instructive because it shows why hunting occurs. As the speed increases, the inertial forces become comparable with the adhesion forces. That is why the critical speed depends on the ratio of the axle load (which determines the adhesion force) to the wheelset mass (which determines the inertial forces).

Alternatively, below a certain speed, the energy which is extracted from the forward motion is insufficient to replace the energy lost by lowering the axles and the motion damps out; above this speed, the energy extracted is greater than the loss in potential energy and the amplitude builds up.

The potential energy at maximum axle yaw may be increased by including an elastic constraint on the yaw motion of the axle, so that there is a contribution arising from spring tension. Arranging wheels in bogies to increase the constraint on the yaw motion of wheelsets and applying elastic constraints to the bogie also raises the critical speed. Introducing elastic forces into the equation permits suspension designs which are limited only by the onset of gross slippage, rather than classical hunting. The penalty to be paid for the virtual elimination of hunting is a straight track, with an attendant right-of-way problem and incompatibility with legacy infrastructure.

Hunting is a dynamic problem which can be solved, in principle at least, by active feedback control, which may be adapted to the quality of track. However, the introduction of active control raises reliability and safety issues.

Shortly after the onset of hunting, gross slippage occurs and the wheel flanges impact on the rails, potentially causing damage to both.

Railway wheelsets

Kinematic analysis

Energy balance

Concluding comments

See also