In astrodynamics

Astrodynamics

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and Newton's law of universal gravitation. It...

 or celestial mechanics

Celestial mechanics

Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...

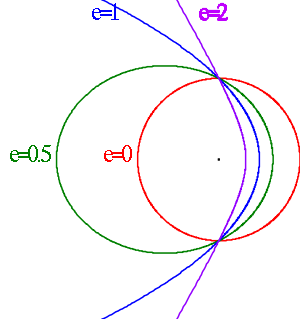
 a hyperbolic trajectory is a Kepler orbit

Kepler orbit

In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...

 with the eccentricity

Orbital eccentricity

The orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...

 greater than 1. Under standard assumptions a body traveling along this trajectory will coast to infinity, arriving there with hyperbolic excess velocity relative to the central body

Central body

In astrodynamics a central body is a body that is being orbited by an secondary body, or satellite .The central body is properly referred to as the primary body.Under standard assumptions in astrodynamics:...

. Similarly to parabolic trajectory

Parabolic trajectory

In astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the eccentricity equal to 1. When moving away from the source it is called an escape orbit, otherwise a capture orbit...

 all hyperbolic trajectories are also escape trajectories. The specific energy

Specific orbital energy

In the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...

 of a hyperbolic trajectory orbit is positive. The shape of a hyperbolic trajectory is a hyperbola

Hyperbola

In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...

.

Hyperbolic excess velocity

Under standard assumptions the body traveling along hyperbolic trajectory will attain in infinity an orbital velocity

Orbital velocity

Orbital velocity can refer to the following:* The orbital speed of a body in a gravitational field.* The velocity of particles due to wave motion, in particular in wind waves....

 called hyperbolic excess velocity () that can be computed as:
where:

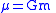• is standard gravitational parameter
  Standard gravitational parameter
  In astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
  
  ,
• is the negative semi-major axis
  Semi-major axis
  The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
  
   of orbit
  Orbit
  In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
  
  's hyperbola
  Hyperbola
  In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
  
  .

The hyperbolic excess velocity is related to the specific orbital energy

Specific orbital energy

In the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...

 or characteristic energy by

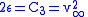
Velocity

Under standard assumptions the orbital velocity

Orbital velocity

Orbital velocity can refer to the following:* The orbital speed of a body in a gravitational field.* The velocity of particles due to wave motion, in particular in wind waves....

 () of a body traveling along hyperbolic trajectory can be computed as (Vallado):
where:

• is standard gravitational parameter
  Standard gravitational parameter
  In astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
  
  ,
• is radial distance of orbiting body from central body
  Central body
  In astrodynamics a central body is a body that is being orbited by an secondary body, or satellite .The central body is properly referred to as the primary body.Under standard assumptions in astrodynamics:...
  
  ,
• is the negative semi-major axis
  Semi-major axis
  The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
  
  .

Under standard assumptions, at any position in the orbit the following relation holds for orbital velocity

Orbital velocity

Orbital velocity can refer to the following:* The orbital speed of a body in a gravitational field.* The velocity of particles due to wave motion, in particular in wind waves....

 (), local escape velocity

Escape velocity

In physics, escape velocity is the speed at which the kinetic energy plus the gravitational potential energy of an object is zero gravitational potential energy is negative since gravity is an attractive force and the potential is defined to be zero at infinity...

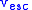() and hyperbolic excess velocity ():

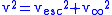
Note that this means that a relatively small extra delta-v

Delta-v

In astrodynamics a Δv or delta-v is a scalar which takes units of speed. It is a measure of the amount of "effort" that is needed to change from one trajectory to another by making an orbital maneuver....

 above that needed to accelerate to the escape speed, results in a relatively large speed at infinity.

Angle between approach and departure

Let the angle between approach and departure (between asymptotes) be .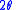
and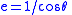

where:

• is the orbital eccentricity, which is greater than 1 for hyperbolic trajectories.

Distance of closest approach

The distance of closest approach, also called the periapse distance and the focal distance, is given by

Energy

Under standard assumptions, specific orbital energy

Specific orbital energy

In the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...

 () of a hyperbolic trajectory is greater than zero and the orbital energy conservation equation for this kind of trajectory takes form: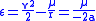
where:

• is orbital velocity
  Orbital velocity
  Orbital velocity can refer to the following:* The orbital speed of a body in a gravitational field.* The velocity of particles due to wave motion, in particular in wind waves....
  
   of orbiting body,
• is radial distance of orbiting body from central body
  Central body
  In astrodynamics a central body is a body that is being orbited by an secondary body, or satellite .The central body is properly referred to as the primary body.Under standard assumptions in astrodynamics:...
  
  ,
• is the negative semi-major axis
  Semi-major axis
  The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
  
  ,
• is standard gravitational parameter
  Standard gravitational parameter
  In astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
  
  .

Radial hyperbolic trajectory

A radial hyperbolic trajectory is a non-periodic trajectory on a straight line

Radial trajectory

In astrodynamics and celestial mechanics a radial trajectory is a Kepler orbit with zero angular momentum. Two objects in a radial trajectory move directly towards or away from each other in a straight line.- Classification :...

 where the relative speed of the two objects always exceeds the escape velocity

Escape velocity

In physics, escape velocity is the speed at which the kinetic energy plus the gravitational potential energy of an object is zero gravitational potential energy is negative since gravity is an attractive force and the potential is defined to be zero at infinity...

. There are two cases: the bodies move away from each other or towards each other. This is a hyperbolic orbit with semi-minor axis = 0 and eccentricity = 1. Although the eccentricity is 1 this is not a parabolic orbit.

External links

• http://homepage.mac.com/sjbradshaw/msc/traject.html
• http://www.go.ednet.ns.ca/~larry/orbits/ellipse.html