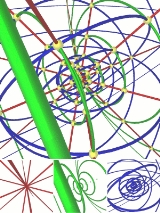
Hypercone
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a hypercone (or spherical cone) is the figure in the 4-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
represented by the equation
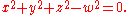
It is a quadric
Quadric
In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
surface, and is one of the possible 3-manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s which are 4-dimensional equivalents of the conical surface
Conical surface
In geometry, a conical surface is the unbounded surface formed by the union of all the straight lines that pass through a fixed point — the apex or vertex — and any point of some fixed space curve — the directrix — that does not contain the apex...
in 3 dimensions. It is also named spherical cone because its intersections with hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
s perpendicular to the w-axis are sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s. A four-dimensional right spherical hypercone can be thought of as a sphere which expands with time, starting its expansion from a single point source, such that the center of the expanding sphere remains fixed. An oblique spherical hypercone would be a sphere which expands with time, again starting its expansion from a point source, but such that the center of the expanding sphere moves with a uniform velocity.
Parametric form
A right spherical hypercone can be described by the function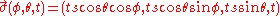
with vertex at the origin and expansion speed s.
An oblique spherical hypercone could then be described by the function

where
 is the 3-velocity of the center of the expanding sphere.
is the 3-velocity of the center of the expanding sphere.An example of such a cone would be an expanding sound wave as seen from the point of view of a moving reference frame: e.g. the sound wave of a jet aircraft
Jet aircraft
A jet aircraft is an aircraft propelled by jet engines. Jet aircraft generally fly much faster than propeller-powered aircraft and at higher altitudes – as high as . At these altitudes, jet engines achieve maximum efficiency over long distances. The engines in propeller-powered aircraft...
as seen from the jet's own reference frame.
Note that the 3D-surfaces above enclose 4D-hypervolumes, which are the 4-cones proper.
Geometrical interpretation
The spherical cone consists of two unbounded nappes, which meet at the origin and are the analogues of the nappes of the 3-dimensional conical surface. The upper nappe corresponds with the half with positive w-coordinates, and the lower nappe corresponds with the half with negative w-coordinates.If it is restricted between the hyperplanes
 and
and  for some non-zero r, then it may be closed by a 3-ball
for some non-zero r, then it may be closed by a 3-ballBall (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
of radius r, centered at (0,0,0,r), so that it bounds a finite 4-dimensional volume. This volume is given by the formula
 , and is the 4-dimensional equivalent of the solid cone
, and is the 4-dimensional equivalent of the solid coneCone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
. The ball may be thought of as the 'lid' at the base of the 4-dimensional cone's nappe, and the origin becomes its 'apex'.
This shape may be projected
Graphical projection
Graphical projection is a protocol by which an image of a three-dimensional object is projected onto a planar surface without the aid of mathematical calculation, used in technical drawing.- Overview :...
into 3-dimensional space in various ways. If projected onto the XYZ hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
, its image is a ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
. If projected onto the XYW, XZW, or YZW hyperplanes, its image is a solid cone
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
. If projected onto an oblique hyperplane, its image is either an ellipsoid or a solid cone with an ellipsoidal base (resembling an ice cream cone
Ice cream cone
An ice cream cone, poke or cornet is a dry, cone-shaped pastry, usually made of a wafer similar in texture to a waffle, allowing ice cream to be eaten without a bowl or spoon...
). These images are the analogues of the possible images of the solid cone projected to 2 dimensions.
Construction
The (half) hypercone may be constructed in a manner analogous to the construction of a 3D cone. A 3D cone may be thought of as the result of stacking progressively smaller discs on top of each other until they taper to a point. Alternatively, a 3D cone may be regarded as the volume swept out by an upright isosceles triangle as it rotates about its base.A 4D hypercone may be constructed analogously: by stacking progressively smaller balls on top of each other in the 4th direction until they taper to a point, or taking the hypervolume swept out by a tetrahedron standing upright in the 4th direction as it rotates freely about its base in the 3D hyperplane on which it rests.
Temporal interpretation
If the w-coordinate of the equation of the spherical cone is interpreted as time, then it is the shape of the light coneLight cone
A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...
in special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
. In this case, the equation is usually written as:
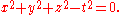
The upper nappe is then the future light cone and the lower nappe is the past light cone.

