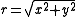Hypot
Encyclopedia
Hypot is a mathematical function defined to calculate the length of the hypotenuse of a right-angle triangle. It was designed to avoid errors arising due to limited-precision calculations performed on computers.
The magnitude of the hypotenuse from (0, 0) to (x, y) can be calculated using:
However the squares of very large or small values of x and y may exceed the range of machine precision when calculated on a computer, leading to an inaccurate result (see underflow
, overflow
). The hypot function was designed to calculate the result without causing this problem.
The hypot function may typically be used together with the atan2
function to convert from Cartesian
to polar coordinates:
This operation is also known as Pythagorean addition.
. A common implementation technique is to exchange the values, if necessary, so that |x| > |y|, and then use the equivalent form:
Motivation and usage
Calculation of the length of the hypotenuse of a triangle is possible to do using the square root function but hypot(x, y) avoids possible problems with very large or very small numbers.The magnitude of the hypotenuse from (0, 0) to (x, y) can be calculated using:
However the squares of very large or small values of x and y may exceed the range of machine precision when calculated on a computer, leading to an inaccurate result (see underflow
Arithmetic underflow
The term arithmetic underflow is a condition in a computer program that can occur when the true result of afloating point operation is smaller in magnitude...
, overflow
Arithmetic overflow
The term arithmetic overflow or simply overflow has the following meanings.# In a computer, the condition that occurs when a calculation produces a result that is greater in magnitude than that which a given register or storage location can store or represent.# In a computer, the amount by which a...
). The hypot function was designed to calculate the result without causing this problem.
The hypot function may typically be used together with the atan2
Atan2
In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
function to convert from Cartesian
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
to polar coordinates:
- r = hypot(x, y) θ = atan2(y, x)
This operation is also known as Pythagorean addition.
Implementation
The difficulty with the naive implementation is that x2 or y2 may over- or underflow, unless the intermediate result is computed with extended precisionExtended precision
The term extended precision refers to storage formats for floating point numbers not falling into the regular sequence of single, double, and quadruple precision formats...
. A common implementation technique is to exchange the values, if necessary, so that |x| > |y|, and then use the equivalent form:
-
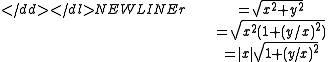
The computation of y/x cannot overflow, and underflows compute the correct result. The square root is computed over a value between 1 and 2. Finally, the multiplication by |x| cannot underflow, and overflows only when the result is too large to represent.
Programming language support
The function is present in several programming languages:- C99C99C99 is a modern dialect of the C programming language. It extends the previous version with new linguistic and library features, and helps implementations make better use of available computer hardware and compiler technology.-History:...
- Python
- Apple's PowerPC Numerics
- MATLAB
- Pascal
- PHP
- Java (since version 1.5)
- Ruby
Some C90 and C++ libraries have provided a hypot function. - C99