
Identity theorem
Encyclopedia
In complex analysis
, a branch of mathematics, the identity theorem for holomorphic function
s states: given functions f and g holomorphic on a connected
open set
D, if f = g on some neighborhood of z that is in D, then f = g on D. Thus a holomorphic function is completely determined by its values on a (possibly quite small) neighborhood in D. This is not true for real-differentiable functions. In comparison, holomorphy, or complex-differentiability, is a much more rigid notion. Informally, one sometimes summarizes the theorem by saying holomorphic functions are "hard" (as opposed to, say, continuous functions which are "soft").
The underpinning fact from which the theorem is established is the developability of a holomorphic function into its Taylor series.
s, the result does not hold). Under this assumption, since we are given that the set is not empty, topologically the claim amounts to that f and g coincide on a set that is both open
and closed
.
The closedness is immediate from the continuity
of f and g.
Therefore, the main issue is to show that the set on which f = g is an open set.
Because a holomorphic function can be represented by its Taylor series everywhere on its domain, it is sufficient to consider the set
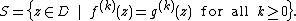
Suppose w lies in S. Then, because the Taylor series of f and g at w have non-zero radius of convergence
, the open disk Br(w) also lies in S for some r. (In fact, r can be anything less than the distance from w to the boundary of D). This shows S is open and proves the theorem.
To prove this, it is enough to show that f(k)(c) = g(k)(c) for all k ≥ 0. If this is not the case, let m be the smallest nonnegative integer with f(m)(c) ≠ g(m)(c). By holomorphy, we have the following Taylor series representation in some open neighborhood of c:
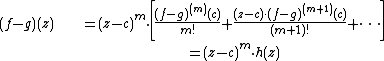
By continuity, h is non-zero in some small open disk B around c. But then f − g ≠ 0 on the punctured set B − {c}. This contradicts the assumption that c is an accumulation point of {f = g} and therefore the claim is proved.
This formulation of the theorem shows that for a complex number a, the fiber f−1(a) is a discrete (and countable) set unless f = a.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a branch of mathematics, the identity theorem for holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s states: given functions f and g holomorphic on a connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
D, if f = g on some neighborhood of z that is in D, then f = g on D. Thus a holomorphic function is completely determined by its values on a (possibly quite small) neighborhood in D. This is not true for real-differentiable functions. In comparison, holomorphy, or complex-differentiability, is a much more rigid notion. Informally, one sometimes summarizes the theorem by saying holomorphic functions are "hard" (as opposed to, say, continuous functions which are "soft").
The underpinning fact from which the theorem is established is the developability of a holomorphic function into its Taylor series.
Proof
The connectedness assumption on the domain D is necessary and is in fact key to a short proof given here (obviously, if D consists of two disjoint open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s, the result does not hold). Under this assumption, since we are given that the set is not empty, topologically the claim amounts to that f and g coincide on a set that is both open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
and closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
.
The closedness is immediate from the continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
of f and g.
Therefore, the main issue is to show that the set on which f = g is an open set.
Because a holomorphic function can be represented by its Taylor series everywhere on its domain, it is sufficient to consider the set
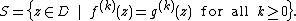
Suppose w lies in S. Then, because the Taylor series of f and g at w have non-zero radius of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
, the open disk Br(w) also lies in S for some r. (In fact, r can be anything less than the distance from w to the boundary of D). This shows S is open and proves the theorem.
An improvement
The hypotheses on this theorem can be relaxed slightly while still producing the same conclusion. Specifically, if two holomorphic functions f and g on a domain D agree on a set which has an accumulation point c in D then f = g on all of D.To prove this, it is enough to show that f(k)(c) = g(k)(c) for all k ≥ 0. If this is not the case, let m be the smallest nonnegative integer with f(m)(c) ≠ g(m)(c). By holomorphy, we have the following Taylor series representation in some open neighborhood of c:
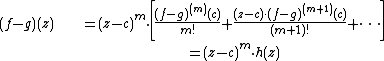
By continuity, h is non-zero in some small open disk B around c. But then f − g ≠ 0 on the punctured set B − {c}. This contradicts the assumption that c is an accumulation point of {f = g} and therefore the claim is proved.
This formulation of the theorem shows that for a complex number a, the fiber f−1(a) is a discrete (and countable) set unless f = a.

