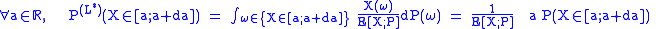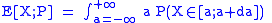Importance sampling
Encyclopedia
In statistics
, importance sampling is a general technique for estimating properties of a particular distribution
, while only having samples generated from a different distribution rather than the distribution of interest. It is related to Umbrella sampling
in computational physics
. Depending on the application, the term may refer to the process of sampling from this alternative distribution, the process of inference, or both.
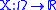 be a random variable
be a random variable
in some probability space
 . We wish to estimate the expected value
. We wish to estimate the expected value
of X under P. If we have random samples , generated according to P, then an empirical estimate of E[X;P] is
, generated according to P, then an empirical estimate of E[X;P] is
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, importance sampling is a general technique for estimating properties of a particular distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
, while only having samples generated from a different distribution rather than the distribution of interest. It is related to Umbrella sampling
Umbrella sampling
Umbrella sampling is a technique in computational physics and chemistry, used to improve sampling of a system where ergodicity is hindered by the form of the system's energy landscape. It was first suggested by Torrie and Valleau in 1977...
in computational physics
Computational physics
Computational physics is the study and implementation of numerical algorithms to solve problems in physics for which a quantitative theory already exists...
. Depending on the application, the term may refer to the process of sampling from this alternative distribution, the process of inference, or both.
Basic theory
More formally, let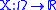 be a random variable
be a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
in some probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
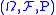 . We wish to estimate the expected value
. We wish to estimate the expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of X under P. If we have random samples
 , generated according to P, then an empirical estimate of E[X;P] is
, generated according to P, then an empirical estimate of E[X;P] is-
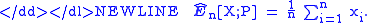
The basic idea of importance sampling is to change the probability P so that the estimation of E[X;P] is easier. Choose a random variable such that E[L;P]=1 and that P-almost everywhereAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
such that E[L;P]=1 and that P-almost everywhereAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
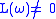 . The variate L defines another probability
. The variate L defines another probability 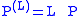 that satisfies
that satisfies
-

The variable X/L will thus be sampled under P(L) to estimate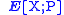 as above. This procedure will improve the estimation when
as above. This procedure will improve the estimation when  . Another case of interest is when X/L is easier to sample under P(L) than X under P.
. Another case of interest is when X/L is easier to sample under P(L) than X under P.
When X is of constant sign over Ω, the best variable L would clearly be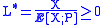 , so that X/L* is the searched constant E[X;P] and a single sample under P(L*) suffices to give its value. Unfortunately we cannot take that choice, because E[X;P] is precisely the value we are looking for! However this theoretical best case L* gives us an insight into what importance sampling does:
, so that X/L* is the searched constant E[X;P] and a single sample under P(L*) suffices to give its value. Unfortunately we cannot take that choice, because E[X;P] is precisely the value we are looking for! However this theoretical best case L* gives us an insight into what importance sampling does:
to the right,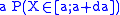 is one of the infinitesimal elements that sum up to E[X;P]:
is one of the infinitesimal elements that sum up to E[X;P]:
therefore, a good probability change P(L) in importance sampling will redistribute the law of X so that its samples' frequencies are sorted directly according to their weights in E[X;P]. Hence the name "importance sampling."
Note that whenever is the uniform distribution and
is the uniform distribution and  , we are just estimating the integral of the real function
, we are just estimating the integral of the real function 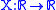 , so the method can also be used for estimating simple integrals.
, so the method can also be used for estimating simple integrals.
Application to probabilistic inference
Such methods are frequently used to estimate posterior densities or expectations in state and/or parameter estimation problems in probabilistic models that are too hard to treat analytically, for example in Bayesian networkBayesian networkA Bayesian network, Bayes network, belief network or directed acyclic graphical model is a probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph . For example, a Bayesian network could represent the probabilistic...
s.
Application to simulation
Importance sampling is a variance reductionVariance reductionIn mathematics, more specifically in the theory of Monte Carlo methods, variance reduction is a procedure used to increase the precision of the estimates that can be obtained for a given number of iterations. Every output random variable from the simulation is associated with a variance which...
technique that can be used in the Monte Carlo methodMonte Carlo methodMonte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
. The idea behind importance sampling is that certain values of the input random variables in a simulationSimulationSimulation is the imitation of some real thing available, state of affairs, or process. The act of simulating something generally entails representing certain key characteristics or behaviours of a selected physical or abstract system....
have more impact on the parameter being estimated than others. If these "important" values are emphasized by sampling more frequently, then the estimatorEstimatorIn statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
variance can be reduced. Hence, the basic methodology in importance sampling is to choose a distribution which "encourages" the important values. This use of "biased" distributions will result in a biased estimator if it is applied directly in the simulation. However, the simulation outputs are weighted to correct for the use of the biased distribution, and this ensures that the new importance sampling estimator is unbiased. The weight is given by the likelihood ratio, that is, the Radon–Nikodym derivative of the true underlying distribution with respect to the biased simulation distribution.
The fundamental issue in implementing importance sampling simulation is the choice of the biased distribution which encourages the important regions of the input variables. Choosing or designing a good biased distribution is the "art" of importance sampling. The rewards for a good distribution can be huge run-time savings; the penalty for a bad distribution can be longer run times than for a general Monte Carlo simulation without importance sampling.
Mathematical approach
Consider estimating by simulation the probability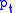 of an event
of an event  , where
, where  is a random variable with distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
is a random variable with distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
 and probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
and probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
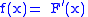 , where prime denotes derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
, where prime denotes derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
. A -length independent and identically distributed (i.i.d.) sequence
-length independent and identically distributed (i.i.d.) sequence 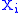 is generated from the distribution
is generated from the distribution  , and the number
, and the number 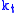 of random variables that lie above the threshold
of random variables that lie above the threshold  are counted. The random variable
are counted. The random variable 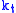 is characterized by the Binomial distribution
is characterized by the Binomial distribution
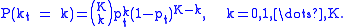
One can show that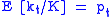 , and
, and 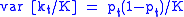 , so in the limit
, so in the limit  we are able to obtain
we are able to obtain 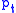 . Note that the variance is low if
. Note that the variance is low if  . Importance sampling is concerned with the determination and use of an alternate density function
. Importance sampling is concerned with the determination and use of an alternate density function  (for X), usually referred to as a biasing density, for the simulation experiment. This density allows the event
(for X), usually referred to as a biasing density, for the simulation experiment. This density allows the event  to occur more frequently, so the sequence lengths
to occur more frequently, so the sequence lengths  gets smaller for a given estimatorEstimatorIn statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
gets smaller for a given estimatorEstimatorIn statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
variance. Alternatively, for a given , use of the biasing density results in a variance smaller than that of the conventional Monte Carlo estimate. From the definition of
, use of the biasing density results in a variance smaller than that of the conventional Monte Carlo estimate. From the definition of 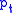 , we can introduce
, we can introduce 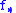 as below.
as below.
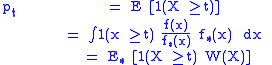
where
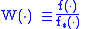
is a likelihood ratio and is referred to as the weighting function. The last equality in the above equation motivates the estimator
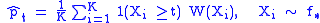
This is the importance sampling estimator of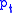 and is unbiased. That is, the estimation procedure is to generate i.i.d. samples from
and is unbiased. That is, the estimation procedure is to generate i.i.d. samples from 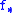 and for each sample which exceeds
and for each sample which exceeds  , the estimate is incremented by the weight
, the estimate is incremented by the weight  evaluated at the sample value. The results are averaged over
evaluated at the sample value. The results are averaged over  trials. The variance of the importance sampling estimator is easily shown to be
trials. The variance of the importance sampling estimator is easily shown to be
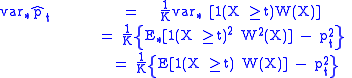
Now, the importance sampling problem then focuses on finding a biasing density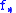 such that the variance of the importance sampling estimator is less than the variance of the general Monte Carlo estimate. For some biasing density function, which minimizes the variance, and under certain conditions reduces it to zero, it is called an optimal biasing density function.
such that the variance of the importance sampling estimator is less than the variance of the general Monte Carlo estimate. For some biasing density function, which minimizes the variance, and under certain conditions reduces it to zero, it is called an optimal biasing density function.
Conventional biasing methods
Although there are many kinds of biasing methods, the following two methods are most widely used in the applications of importance sampling.
Scaling
Shifting probability mass into the event region by positive scaling of the random variable
by positive scaling of the random variable  with a number greater than unity has the effect of increasing the variance (mean also) of the density function. This results in a heavier tail of the density, leading to an increase in the event probability. Scaling is probably one of the earliest biasing methods known and has been extensively used in practice. It is simple to implement and usually provides conservative simulation gains as compared to other methods.
with a number greater than unity has the effect of increasing the variance (mean also) of the density function. This results in a heavier tail of the density, leading to an increase in the event probability. Scaling is probably one of the earliest biasing methods known and has been extensively used in practice. It is simple to implement and usually provides conservative simulation gains as compared to other methods.
In importance sampling by scaling, the simulation density is chosen as the density function of the scaled random variable , where usually
, where usually  for tail probability estimation. By transformation,
for tail probability estimation. By transformation,
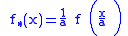
and the weighting function is
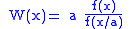
While scaling shifts probability mass into the desired event region, it also pushes mass into the complementary region which is undesirable. If
which is undesirable. If  is a sum of
is a sum of  random variables, the spreading of mass takes place in an
random variables, the spreading of mass takes place in an  dimensional space. The consequence of this is a decreasing importance sampling gain for increasing
dimensional space. The consequence of this is a decreasing importance sampling gain for increasing  , and is called the dimensionality effect.
, and is called the dimensionality effect.
Translation
Another simple and effective biasing technique employs translation of the density function (and hence random variable) to place much of its probability mass in the rare event region. Translation does not suffer from a dimensionality effect and has been successfully used in several applications relating to simulation of digital communication systems. It often provides better simulation gains than scaling. In biasing by translation, the simulation density is given by
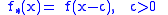
where is the amount of shift and is to be chosen to minimize the variance of the importance sampling estimator.
is the amount of shift and is to be chosen to minimize the variance of the importance sampling estimator.
Effects of system complexity
The fundamental problem with importance sampling is that designing good biased distributions becomes more complicated as the system complexity increases. Complex systems are the systems with long memory since complex processing of a few inputs is much easier to handle. This dimensionality or memory can cause problems in three ways:
- long memory (severe intersymbol interferenceIntersymbol interferenceIn telecommunication, intersymbol interference is a form of distortion of a signal in which one symbol interferes with subsequent symbols. This is an unwanted phenomenon as the previous symbols have similar effect as noise, thus making the communication less reliable...
(ISI)) - unknown memory (Viterbi decoderViterbi decoderA Viterbi decoder uses the Viterbi algorithm for decoding a bitstream that has beenencoded using forward error correction based on a convolutional code....
s) - possibly infinite memory (adaptive equalizers)
In principle, the importance sampling ideas remain the same in these situations, but the design becomes much harder. A successful approach to combat this problem is essentially breaking down a simulation into several smaller, more sharply defined subproblems. Then importance sampling strategies are used to target each of the simpler subproblems. Examples of techniques to break the simulation down are conditioning and error-event simulation (EES) and regenerative simulation.
Evaluation of importance sampling
In order to identify successful importance sampling techniques, it is useful to be able to quantify the run-time savings due to the use of the importance sampling approach. The performance measure commonly used is , and this can be interpreted as the speed-up factor by which the importance sampling estimator achieves the same precision as the MC estimator. This has to be computed empirically since the estimator variances are not likely to be analytically possible when their mean is intractable. Other useful concepts in quantifying an importance sampling estimator are the variance bounds and the notion of asymptotic efficiency.
, and this can be interpreted as the speed-up factor by which the importance sampling estimator achieves the same precision as the MC estimator. This has to be computed empirically since the estimator variances are not likely to be analytically possible when their mean is intractable. Other useful concepts in quantifying an importance sampling estimator are the variance bounds and the notion of asymptotic efficiency.
Variance cost function
Variance is not the only possible cost function for a simulation, and other cost functions, such as the mean absolute deviation, are used in various statistical applications. Nevertheless, the variance is the primary cost function addressed in the literature, probably due to the use of variances in confidence intervalConfidence intervalIn statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
s and in the performance measure .
.
An associated issue is the fact that the ratio overestimates the run-time savings due to importance sampling since it does not include the extra computing time required to compute the weight function. Hence, some people evaluate the net run-time improvement by various means. Perhaps a more serious overhead to importance sampling is the time taken to devise and program the technique and analytically derive the desired weight function.
overestimates the run-time savings due to importance sampling since it does not include the extra computing time required to compute the weight function. Hence, some people evaluate the net run-time improvement by various means. Perhaps a more serious overhead to importance sampling is the time taken to devise and program the technique and analytically derive the desired weight function.
See also
- Monte Carlo methodMonte Carlo methodMonte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
- variance reductionVariance reductionIn mathematics, more specifically in the theory of Monte Carlo methods, variance reduction is a procedure used to increase the precision of the estimates that can be obtained for a given number of iterations. Every output random variable from the simulation is associated with a variance which...
- Stratified samplingStratified samplingIn statistics, stratified sampling is a method of sampling from a population.In statistical surveys, when subpopulations within an overall population vary, it is advantageous to sample each subpopulation independently. Stratification is the process of dividing members of the population into...
- Recursive stratified sampling
- Particle filterParticle filterIn statistics, particle filters, also known as Sequential Monte Carlo methods , are sophisticated model estimation techniques based on simulation...
— a sequential Monte Carlo method, which uses importance sampling - Auxiliary field Monte CarloAuxiliary field Monte CarloAuxiliary field Monte Carlo is a method that allows the calculation, by use of Monte Carlo techniques, of averages of operators in many-body quantum mechanical or classical problems .-Reweighting procedure and numerical sign problem:The distinctive ingredient of "auxiliary field Monte Carlo" is...
- Rejection samplingRejection samplingIn mathematics, rejection sampling is a basic pseudo-random number sampling technique used to generate observations from a distribution. It is also commonly called the acceptance-rejection method or "accept-reject algorithm"....
External links
- Sequential Monte Carlo Methods (Particle Filtering) homepage on University of Cambridge
- Introduction to importance sampling in rare-event simulations European journal of Physics. PDF document.
- Adaptive monte carlo methods for rare event simulation: adaptive monte carlo methods for rare event simulations Winter Simulation Conference
-
-