Impulse invariance
Encyclopedia
Impulse invariance is a technique for designing discrete-time infinite-impulse-response (IIR) filters from continuous-time filters in which the impulse response of the continuous-time system is sampled to produce the impulse response of the discrete-time system. The frequency response of the discrete-time system will be a sum of shifted copies of the frequency response of the continuous-time system; if the continuous-time system is approximately band-limited to a frequency less than the Nyquist frequency
of the sampling, then the frequency response of the discrete-time system will be approximately equal to it for frequencies below the Nyquist frequency.
, is sampled with sampling period 
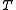to produce the discrete-time system's impulse response, 
.
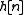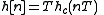
Thus, the frequency responses of the two systems are related by
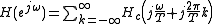
If the continuous time filter is approximately band-limited (i.e.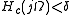
when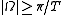 
), then the frequency response of the discrete-time system will be approximately the continuous-time system's frequency response for frequencies below π radians per sample (below the Nyquist frequency 1/(2T) Hz):
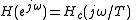for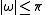 
is an alternative to impulse invariance that uses a different mapping that maps the continuous-time system's frequency response, out to infinite frequency, into the range of frequencies up to the Nyquist frequency in the discrete-time case, as opposed to mapping frequencies linearly with circular overlap as impulse invariance does.
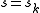, the system function can be written in partial fraction expansion as
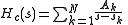
Thus, using the inverse Laplace transform, the impulse response is
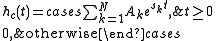
The corresponding discrete-time system's impulse response is then defined as the following
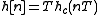
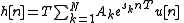
Performing a z-transform on the discrete-time impulse response produces the following discrete-time system function
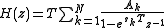
Thus the poles from the continuous-time system function are translated to poles at z = eskT. The zeros, if any, are not so simply mapped.
, or pole–zero mapping. In the case of all-pole filters, the methods are equivalent.
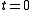, the expressions above are not consistent.
This is because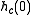
should really only contribute half its value to 
.
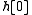Making this correction gives
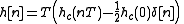
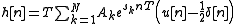
Performing a z-transform on the discrete-time impulse response produces the following discrete-time system function
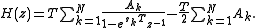
Nyquist frequency
The Nyquist frequency, named after the Swedish-American engineer Harry Nyquist or the Nyquist–Shannon sampling theorem, is half the sampling frequency of a discrete signal processing system...
of the sampling, then the frequency response of the discrete-time system will be approximately equal to it for frequencies below the Nyquist frequency.
Discussion
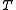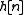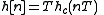
The continuous-time system's impulse response,, is sampled with sampling period to produce the discrete-time system's impulse response, .Thus, the frequency responses of the two systems are related by
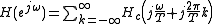
If the continuous time filter is approximately band-limited (i.e.
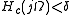when 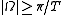), then the frequency response of the discrete-time system will be approximately the continuous-time system's frequency response for frequencies below π radians per sample (below the Nyquist frequency 1/(2T) Hz): 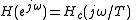for 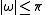Comparison to the bilinear transform
Note that aliasing will occur, including aliasing below the Nyquist frequency to the extent that the continuous-time filter's response is nonzero above that frequency. The bilinear transformBilinear transform
The bilinear transform is used in digital signal processing and discrete-time control theory to transform continuous-time system representations to discrete-time and vice versa....
is an alternative to impulse invariance that uses a different mapping that maps the continuous-time system's frequency response, out to infinite frequency, into the range of frequencies up to the Nyquist frequency in the discrete-time case, as opposed to mapping frequencies linearly with circular overlap as impulse invariance does.
Effect on poles in system function
If the continuous poles at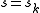, the system function can be written in partial fraction expansion as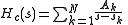Thus, using the inverse Laplace transform, the impulse response is
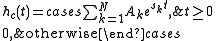
The corresponding discrete-time system's impulse response is then defined as the following
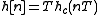
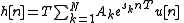
Performing a z-transform on the discrete-time impulse response produces the following discrete-time system function
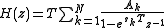
Thus the poles from the continuous-time system function are translated to poles at z = eskT. The zeros, if any, are not so simply mapped.
Poles and zeros
If the system function has zeros as well as poles, they can be mapped the same way, but the result is no longer an impulse invariance result: the discrete-time impulse response is not equal simply to samples of the continuous-time impulse response. This method is known as the matched Z-transform methodMatched Z-transform method
The matched Z-transform method, also called the pole–zero mapping or pole–zero matching method, is a technique for converting a continuous-time filter design to a discrete-time filter design....
, or pole–zero mapping. In the case of all-pole filters, the methods are equivalent.
Stability and causality
Since poles in the continuous-time system at s = sk transform to poles in the discrete-time system at z = exp(skT), poles in the left half of the s-plane map to inside the unit circle in the z-plane; so if the continuous-time filter is causal and stable, then the discrete-time filter will be causal and stable as well.Corrected formula
When a causal continuous-time impulse response has a discontinuity at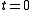, the expressions above are not consistent.This is because
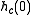should really only contribute half its value to 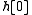.Making this correction gives
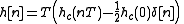
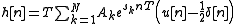
Performing a z-transform on the discrete-time impulse response produces the following discrete-time system function
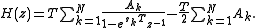
See also
- Infinite impulse responseInfinite impulse responseInfinite impulse response is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time...
- Bilinear transformBilinear transformThe bilinear transform is used in digital signal processing and discrete-time control theory to transform continuous-time system representations to discrete-time and vice versa....
- Matched Z-transform methodMatched Z-transform methodThe matched Z-transform method, also called the pole–zero mapping or pole–zero matching method, is a technique for converting a continuous-time filter design to a discrete-time filter design....
- Continuous-time filters:
- Chebyshev filterChebyshev filterChebyshev filters are analog or digital filters having a steeper roll-off and more passband ripple or stopband ripple than Butterworth filters...
- Butterworth filterButterworth filterThe Butterworth filter is a type of signal processing filter designed to have as flat a frequency response as possible in the passband so that it is also termed a maximally flat magnitude filter...
- Elliptic filterElliptic filterAn elliptic filter is a signal processing filter with equalized ripple behavior in both the passband and the stopband...
- Chebyshev filter
Other sources
- Oppenheim, Alan V. and Schafer, Ronald W. with Buck, John R. Discrete-Time Signal Processing. Second Edition. Upper Saddle River, New Jersey: Prentice-Hall, 1999.
- Sahai, Anant. Course Lecture. Electrical Engineering 123: Digital Signal Processing. University of California, Berkeley. 5 April 2007.
External links
- Impulse Invariant Transform at CircuitDesign.info Brief explanation, an example, and application to Continuous TimeContinuous signalA continuous signal or a continuous-time signal is a varying quantity whose domain, which is often time, is a continuum . That is, the function's domain is an uncountable set. The function itself need not be continuous...
Sigma DeltaSigma DeltaSigma Delta is a local sorority at Dartmouth College in Hanover, New Hampshire, United States. First established on the campus in 1972, Sigma Delta, known as "Sigma Delt" by students, as a chapter of the national sorority Sigma Kappa. Dartmouth's Sigma Kappa chapter was the first sorority to be...
ADC's.