Continuous signal
Encyclopedia
A continuous signal or a continuous-time signal is a varying quantity (a signal)
whose domain, which is often time, is a continuum (e.g., a connected
interval of the reals
). That is, the function's domain is an uncountable set
. The function itself need not be continuous
. To contrast, a discrete time
signal has a countable
domain, like the natural number
s.
The signal is defined over a domain, which may or may not be finite, and there is a functional mapping from the domain to the value of the signal. The continuity of the time variable, in connection with the law of density of real numbers, means that the signal value can be found at any arbitrary point in time.
A typical example of an infinite duration signal is:
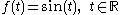
A finite duration counterpart of the above signal could be:
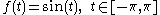and 
otherwise.
The value of a finite (or infinite) duration signal may or may not be finite. For example,
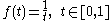and 
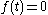otherwise,
is a finite duration signal but it takes an infinite value for
.
In many disciplines, the convention is that a continuous signal must always have a finite value, which makes more sense in the case of physical signals.
For some purposes, infinite singularities are acceptable as long as the signal is integrable over any finite interval (for example, the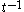
signal is not integrable, but 
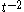is).
Any analogue signal is continuous by nature. Discrete signal
s, used in digital signal processing
, can be obtained by sampling
and quantization
of continuous signals.
Continuous signal may also be defined over an independent variable other than time. Another very common independent variable is space and is particularly useful in image processing
, where two space dimensions are used.
whose domain, which is often time, is a continuum (e.g., a connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
interval of the reals
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
). That is, the function's domain is an uncountable set
Uncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
. The function itself need not be continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. To contrast, a discrete time
Discrete time
Discrete time is the discontinuity of a function's time domain that results from sampling a variable at a finite interval. For example, consider a newspaper that reports the price of crude oil once every day at 6:00AM. The newspaper is described as sampling the cost at a frequency of once per 24...
signal has a countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
domain, like the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s.
The signal is defined over a domain, which may or may not be finite, and there is a functional mapping from the domain to the value of the signal. The continuity of the time variable, in connection with the law of density of real numbers, means that the signal value can be found at any arbitrary point in time.
A typical example of an infinite duration signal is:
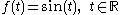
A finite duration counterpart of the above signal could be:
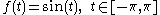and otherwise.The value of a finite (or infinite) duration signal may or may not be finite. For example,
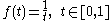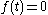and otherwise,is a finite duration signal but it takes an infinite value for
.In many disciplines, the convention is that a continuous signal must always have a finite value, which makes more sense in the case of physical signals.
For some purposes, infinite singularities are acceptable as long as the signal is integrable over any finite interval (for example, the
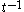signal is not integrable, but 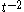is).Any analogue signal is continuous by nature. Discrete signal
Discrete signal
A discrete signal or discrete-time signal is a time series consisting of a sequence of qualities...
s, used in digital signal processing
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
, can be obtained by sampling
Sampling (signal processing)
In signal processing, sampling is the reduction of a continuous signal to a discrete signal. A common example is the conversion of a sound wave to a sequence of samples ....
and quantization
Quantization (signal processing)
Quantization, in mathematics and digital signal processing, is the process of mapping a large set of input values to a smaller set – such as rounding values to some unit of precision. A device or algorithmic function that performs quantization is called a quantizer. The error introduced by...
of continuous signals.
Continuous signal may also be defined over an independent variable other than time. Another very common independent variable is space and is particularly useful in image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
, where two space dimensions are used.