
Infinite expression (mathematics)
Encyclopedia
In mathematics
, an infinite expression is an expression
in which some operators take an infinite number of arguments, or in which the nesting of the operators continues to an infinite depth. A generic concept for infinite expression can lead to ill-defined or self-inconsistent constructions (much like a set of all sets
), but there are several instances of infinite expressions that are well defined.
Examples of well-defined infinite expressions include infinite sums, whether expressed using summation
notation or as an infinite series
, such as
infinite products, whether expressed using product notation or expanded, such as
infinite nested radicals, such as
infinite power towers, such as
and infinite continued fraction
s, whether expressed using Gauss
's Kettenbruch
notation or expanded, such as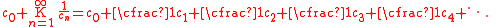
In infinitary logic
, one can use infinite conjunctions and infinite disjunctions.
Even for well-defined infinite expressions, the value of the infinite expression may be ambiguous or not well defined; for instance, there are multiple summation rules available for assigning values to series, and the same series may have different values according to different summation rules if the series is not absolutely convergent
.
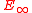 is obtained in every case from the sequence
is obtained in every case from the sequence  of finite expressions, by evaluating the sequence at a hypernatural value
of finite expressions, by evaluating the sequence at a hypernatural value  of the index n, and applying the standard part, so that
of the index n, and applying the standard part, so that  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an infinite expression is an expression
Expression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
in which some operators take an infinite number of arguments, or in which the nesting of the operators continues to an infinite depth. A generic concept for infinite expression can lead to ill-defined or self-inconsistent constructions (much like a set of all sets
Universal set
In set theory, a universal set is a set which contains all objects, including itself. In set theory as usually formulated, the conception of a set of all sets leads to a paradox...
), but there are several instances of infinite expressions that are well defined.
Examples of well-defined infinite expressions include infinite sums, whether expressed using summation
Summation
Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
notation or as an infinite series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
, such as

infinite products, whether expressed using product notation or expanded, such as

infinite nested radicals, such as
infinite power towers, such as
and infinite continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s, whether expressed using Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
's Kettenbruch
Generalized continued fraction
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary real or complex values....
notation or expanded, such as
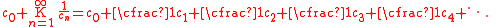
In infinitary logic
Infinitary logic
An infinitary logic is a logic that allows infinitely long statements and/or infinitely long proofs. Some infinitary logics may have different properties from those of standard first-order logic. In particular, infinitary logics may fail to be compact or complete. Notions of compactness and...
, one can use infinite conjunctions and infinite disjunctions.
Even for well-defined infinite expressions, the value of the infinite expression may be ambiguous or not well defined; for instance, there are multiple summation rules available for assigning values to series, and the same series may have different values according to different summation rules if the series is not absolutely convergent
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
.
From the hyperreal viewpoint
From the point of view of the hyperreals, such an infinite expression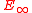 is obtained in every case from the sequence
is obtained in every case from the sequence  of finite expressions, by evaluating the sequence at a hypernatural value
of finite expressions, by evaluating the sequence at a hypernatural value  of the index n, and applying the standard part, so that
of the index n, and applying the standard part, so that  .
.See also
- Iterated binary operationIterated binary operationIn mathematics, an iterated binary operation is an extension of a binary operation on a set S to a function on finite sequences of elements of S through repeated application. Common examples include the extension of the addition operation to the summation operation, and the extension of the...
, large operator - Iterated functionIterated functionIn mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
- IterationIterationIteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
- Dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
- Infinite word
- SequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
- Decimal expansion
- Power series
- Analytic functionAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
- Quasi-analytic function



