Iterated binary operation
Encyclopedia
In mathematics
, an iterated binary operation is an extension of a binary operation
on a set S to a function
on finite sequence
s of elements of S through repeated application. Common examples include the extension of the addition
operation to the summation
operation, and the extension of the multiplication
operation to the product
operation. Other operations, e.g., the set theoretic operations union
and intersection
, are also often iterated, but the iterations are not given separate names. In print, summation and product are represented by special symbols; but other iterated operators often are denoted by larger variants of the symbol for the ordinary binary operator. Thus, the iterations of the four operations mentioned above are denoted
More generally, iteration of a binary function is generally denoted by a forward slash: iteration of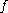
over the sequence 
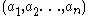is denoted by 
.
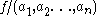In general, there is more than one way to extend a binary operation to operate on finite sequences, depending on whether the operator is associative, and whether the operator has identity element
s.
For , define a new function Fl on finite nonempty sequences of elements of S, where
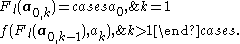
Similarly, define
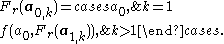
If f has a unique left identity e, the definition of Fl can be modified to operate on empty sequences by defining the value of Fl on an empty sequence to be e (the previous base case on sequences of length 1 becomes redundant). Similarly, Fr can be modified to operate on empty sequences if f has a unique right identity.
If f is associative, then Fl equals Fr, and we can simply write F. Moreover, if an identity element e exists, then it is unique (see Monoid
).
If f is commutative and associative, then F can operate on any non-empty finite multiset
by applying it to an arbitrary enumeration of the multiset. If f moreover has an identity element e, then this is defined to be the value of F on an empty multiset. If f is idempotent, then the above definitions can be extended to finite sets.
If S also is equipped with a metric
or more generally with topology
that is Hausdorff
, so that the concept of a limit of a sequence
is defined in S, then an infinite iteration on a countable sequence in S is defined exactly when the corresponding sequence of finite iterations converges. Thus, e.g., if a0, a1, a2, a3, ... is an infinite sequence of real numbers, then the infinite product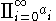
is defined, and equal to 
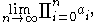if and only if that limit exists.
. The act of iterating on a non-associative binary operation may be represented as a binary tree
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an iterated binary operation is an extension of a binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
on a set S to a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on finite sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of elements of S through repeated application. Common examples include the extension of the addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
operation to the summation
Summation
Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
operation, and the extension of the multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
operation to the product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
operation. Other operations, e.g., the set theoretic operations union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
and intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
, are also often iterated, but the iterations are not given separate names. In print, summation and product are represented by special symbols; but other iterated operators often are denoted by larger variants of the symbol for the ordinary binary operator. Thus, the iterations of the four operations mentioned above are denoted
-
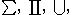and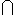 
, respectively.
More generally, iteration of a binary function is generally denoted by a forward slash: iteration of
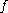over the sequence 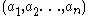is denoted by 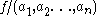.In general, there is more than one way to extend a binary operation to operate on finite sequences, depending on whether the operator is associative, and whether the operator has identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
s.
Definition
Denote by aj,k, with and , the finite sequence of length of elements of S, with members (ai), for . Note that if , the sequence is empty.For , define a new function Fl on finite nonempty sequences of elements of S, where
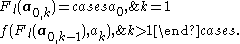
Similarly, define
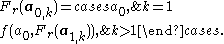
If f has a unique left identity e, the definition of Fl can be modified to operate on empty sequences by defining the value of Fl on an empty sequence to be e (the previous base case on sequences of length 1 becomes redundant). Similarly, Fr can be modified to operate on empty sequences if f has a unique right identity.
If f is associative, then Fl equals Fr, and we can simply write F. Moreover, if an identity element e exists, then it is unique (see Monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
).
If f is commutative and associative, then F can operate on any non-empty finite multiset
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
by applying it to an arbitrary enumeration of the multiset. If f moreover has an identity element e, then this is defined to be the value of F on an empty multiset. If f is idempotent, then the above definitions can be extended to finite sets.
If S also is equipped with a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
or more generally with topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
that is Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, so that the concept of a limit of a sequence
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
is defined in S, then an infinite iteration on a countable sequence in S is defined exactly when the corresponding sequence of finite iterations converges. Thus, e.g., if a0, a1, a2, a3, ... is an infinite sequence of real numbers, then the infinite product
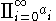is defined, and equal to 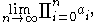if and only if that limit exists.Non-associative binary operation
The general, non-associative binary operation is given by a magmaMagma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
. The act of iterating on a non-associative binary operation may be represented as a binary tree
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
.
See also
- Fold (higher-order function)Fold (higher-order function)In functional programming, fold – also known variously as reduce, accumulate, compress, or inject – are a family of higher-order functions that analyze a recursive data structure and recombine through use of a given combining operation the results of recursively processing its...
- Infinite series
- Infinite product
- Continued fractionContinued fractionIn mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...