Infinity (philosophy)
Encyclopedia
In philosophy
, infinity can be attributed to space and time, as for instance in Kant
's first antinomy
. In both theology and philosophy, infinity is explored in articles such as the Ultimate, the Absolute
, God
, and Zeno's paradoxes
. In Greek philosophy
, for example in Anaximander
, 'the Boundless' is the origin of all that is. He took the beginning or first principle to be an endless, unlimited primordial mass (απιρον, apeiron). In Judeo-Christian theology, for example in the work of theologians such as Duns Scotus
, the infinite nature of God invokes a sense of being without constraint, rather than a sense of being unlimited in quantity. In ethics
infinity plays an important role designating that which cannot be defined or reduced to knowledge or power.
of the Yajurveda
(c. 4th to 3rd century BC) states that "if you remove a part from infinity or add a part to infinity, still what remains is infinity".
The essence of this verse is that the Infinite cannot be measured arithmetically. The Infinite can be represented in Infinite ways and does manifest in infinite ways.
The Indian mathematical
text Surya Prajnapti (c. 400 BC
) classifies all numbers into three sets: enumerable, innumerable, and infinite. Each of these was further subdivided into three orders:
The Jains
were the first to discard the idea that all infinites were the same or equal. They recognized different types of infinities: infinite in length (one dimension
), infinite in area (two dimensions), infinite in volume (three dimensions), and infinite perpetually (infinite number of dimensions).
According to Singh (1987), Joseph (2000) and Agrawal (2000), the highest enumerable number N of the Jains corresponds to the modern concept of aleph-null
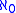(the cardinal number
of the infinite set of integers 1, 2, ...), the smallest cardinal transfinite number
. The Jains also defined a whole system of infinite cardinal numbers, of which the highest enumerable number N is the smallest.
In the Jaina work on the theory of sets
, two basic types of infinite numbers are distinguished. On both physical and ontological
grounds, a distinction was made between ("countless, innumerable") and ananta ("endless, unlimited"), between rigidly bounded and loosely bounded infinities.
:
This is often called potential infinity; however there are two ideas mixed up with this. One is that it is always possible to find a number of things that surpasses any given number, even if there are not actually such things. The other is that we may quantify over infinite sets without restriction. For example,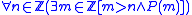
, which reads, "for any integer
n, there exists an integer m > n such that P(m)". The second view is found in a clearer form by medieval writers such as William of Ockham
:
The parts are actually there, in some sense. However, on this view, no infinite magnitude can have a number, for whatever number we can imagine, there is always a larger one: "There are not so many (in number) that there are no more." Aquinas
also argued against the idea that infinity could be in any sense complete, or a totality.
was the first to notice that we can place an infinite set into one-to-one correspondence with one of its proper subsets (any part of the set, that is not the whole). For example, we can match up the set of square number
s {1, 4, 9, 16, ...} with the natural number
s {1, 2, 3, 4, ...} as follows:
It appeared, by this reasoning, as though a set which is naturally smaller than the set of which it is a part (since it does not contain all the members of that set) is in some sense the same "size". Galileo thought this was one of the difficulties which arise when we try, "with our finite minds," to comprehend the infinite.
The idea that size can be measured by one-to-one correspondence is today known as Hume's principle
, although Hume, like Galileo, believed the principle could not be applied to infinite sets. (Mathematicians from the time of Georg Cantor
do apply the principle to infinite sets, and do have a notion of some infinite quantities being greater than others.)
Locke
, in common with most of the empiricist philosophers, also believed that we can have no proper idea of the infinite. They believed all our ideas were derived from sense data
or "impressions," and since all sensory impressions are inherently finite, so too are our thoughts and ideas. Our idea of infinity is merely negative or privative.
Famously, the ultra-empiricist Hobbes
tried to defend the idea of a potential infinity in light of the discovery, by Evangelista Torricelli
, of a figure (Gabriel's Horn
) whose surface area
is infinite, but whose volume
is finite. Not reported, this motivation of Hobbes came too late as curve
s having infinite length yet bounding finite areas were known much before. Such seeming paradoxes are resolved by taking any finite figure and stretching its content infinitely in one direction; the magnitude of its content is unchanged as its divisions drop off geometrically but the magnitude of its bounds increases to infinity by necessity. Potentiality lies in the definitions of this operation, as well-defined
and interconsistent mathematical axioms. A potential infinity is allowed by letting an infinitely-large quantity be cancelled out by an infinitely-small quantity.
, who made an impassioned attack upon axiomatic set theory, and upon the idea of the actual infinite, during his "middle period".
Unlike the traditional empiricists, he thought that the infinite was in some way given to sense experience.
uses infinity to designate that which cannot be defined or reduced to knowledge or power. In Levinas' magnum opus Totality and Infinity
he says,
exist and there are scientists who hold that none of the three exists. And in between there are the various possibilities. Rudy Rucker
, in his book Infinity and the Mind — the Science and Philosophy of the Infinite (1982), has worked out a model list of representatives of each of the eight possible standpoints. The footnote on p. 335 of his book suggests the consideration of the following names: Abraham Robinson
, Plato
, Thomas Aquinas
, L.E.J. Brouwer, David Hilbert
, Bertrand Russell
, Kurt Gödel
and Georg Cantor
.
Philosophy
Philosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
, infinity can be attributed to space and time, as for instance in Kant
Immanuel Kant
Immanuel Kant was a German philosopher from Königsberg , researching, lecturing and writing on philosophy and anthropology at the end of the 18th Century Enlightenment....
's first antinomy
Antinomy
Antinomy literally means the mutual incompatibility, real or apparent, of two laws. It is a term used in logic and epistemology....
. In both theology and philosophy, infinity is explored in articles such as the Ultimate, the Absolute
Absolute (philosophy)
The Absolute is the concept of an unconditional reality which transcends limited, conditional, everyday existence. It is sometimes used as an alternate term for "God" or "the Divine", especially, but by no means exclusively, by those who feel that the term "God" lends itself too easily to...
, God
God
God is the English name given to a singular being in theistic and deistic religions who is either the sole deity in monotheism, or a single deity in polytheism....
, and Zeno's paradoxes
Zeno's paradoxes
Zeno's paradoxes are a set of problems generally thought to have been devised by Greek philosopher Zeno of Elea to support Parmenides's doctrine that "all is one" and that, contrary to the evidence of our senses, the belief in plurality and change is mistaken, and in particular that motion is...
. In Greek philosophy
Greek philosophy
Ancient Greek philosophy arose in the 6th century BCE and continued through the Hellenistic period, at which point Ancient Greece was incorporated in the Roman Empire...
, for example in Anaximander
Anaximander
Anaximander was a pre-Socratic Greek philosopher who lived in Miletus, a city of Ionia; Milet in modern Turkey. He belonged to the Milesian school and learned the teachings of his master Thales...
, 'the Boundless' is the origin of all that is. He took the beginning or first principle to be an endless, unlimited primordial mass (απιρον, apeiron). In Judeo-Christian theology, for example in the work of theologians such as Duns Scotus
Duns Scotus
Blessed John Duns Scotus, O.F.M. was one of the more important theologians and philosophers of the High Middle Ages. He was nicknamed Doctor Subtilis for his penetrating and subtle manner of thought....
, the infinite nature of God invokes a sense of being without constraint, rather than a sense of being unlimited in quantity. In ethics
Ethics
Ethics, also known as moral philosophy, is a branch of philosophy that addresses questions about morality—that is, concepts such as good and evil, right and wrong, virtue and vice, justice and crime, etc.Major branches of ethics include:...
infinity plays an important role designating that which cannot be defined or reduced to knowledge or power.
Early Indian views of infinity
The Isha UpanishadIsha Upanishad
The Isha Upanishad is one of the shortest of the Upanishads, consisting of 17 or 18 verses in total; like other core texts of the vedanta, it is considered revealed scripture by diverse traditions within Hinduism...
of the Yajurveda
Yajurveda
The Yajurveda, a tatpurusha compound of "sacrificial formula', + ) is the third of the four canonical texts of Hinduism, the Vedas. By some, it is estimated to have been composed between 1400 and 1000 BC, the Yajurveda 'Samhita', or 'compilation', contains the liturgy needed to perform the...
(c. 4th to 3rd century BC) states that "if you remove a part from infinity or add a part to infinity, still what remains is infinity".
| पूर्णमदः पूर्णमिदं | , | That is whole, this is whole |
| पूर्णात् पूर्णमुदच्यते | , | From the whole, the whole arises |
| पूर्णस्य पूर्णमादाय | , | When the whole is taken from the whole |
| पूर्णमेवावशिष्यते | , | The whole still will remain. |
The essence of this verse is that the Infinite cannot be measured arithmetically. The Infinite can be represented in Infinite ways and does manifest in infinite ways.
The Indian mathematical
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
text Surya Prajnapti (c. 400 BC
400 BC
Year 400 BC was a year of the pre-Julian Roman calendar. At the time, it was known as the Year of the Tribunate of Esquilinus, Capitolinus, Vulso, Medullinus, Saccus and Vulscus...
) classifies all numbers into three sets: enumerable, innumerable, and infinite. Each of these was further subdivided into three orders:
- Enumerable: lowest, intermediate and highest
- Innumerable: nearly innumerable, truly innumerable and innumerably innumerable
- Infinite: nearly infinite, truly infinite, infinitely infinite
The Jains
Jainism
Jainism is an Indian religion that prescribes a path of non-violence towards all living beings. Its philosophy and practice emphasize the necessity of self-effort to move the soul towards divine consciousness and liberation. Any soul that has conquered its own inner enemies and achieved the state...
were the first to discard the idea that all infinites were the same or equal. They recognized different types of infinities: infinite in length (one dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
), infinite in area (two dimensions), infinite in volume (three dimensions), and infinite perpetually (infinite number of dimensions).
According to Singh (1987), Joseph (2000) and Agrawal (2000), the highest enumerable number N of the Jains corresponds to the modern concept of aleph-null
Aleph number
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
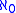(the cardinal numberCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
of the infinite set of integers 1, 2, ...), the smallest cardinal transfinite number
Transfinite number
Transfinite numbers are numbers that are "infinite" in the sense that they are larger than all finite numbers, yet not necessarily absolutely infinite. The term transfinite was coined by Georg Cantor, who wished to avoid some of the implications of the word infinite in connection with these...
. The Jains also defined a whole system of infinite cardinal numbers, of which the highest enumerable number N is the smallest.
In the Jaina work on the theory of sets
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, two basic types of infinite numbers are distinguished. On both physical and ontological
Ontology
Ontology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...
grounds, a distinction was made between ("countless, innumerable") and ananta ("endless, unlimited"), between rigidly bounded and loosely bounded infinities.
Early European views of infinity
In Europe the traditional view derives from AristotleAristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
:
This is often called potential infinity; however there are two ideas mixed up with this. One is that it is always possible to find a number of things that surpasses any given number, even if there are not actually such things. The other is that we may quantify over infinite sets without restriction. For example,
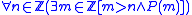, which reads, "for any integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n, there exists an integer m > n such that P(m)". The second view is found in a clearer form by medieval writers such as William of Ockham
William of Ockham
William of Ockham was an English Franciscan friar and scholastic philosopher, who is believed to have been born in Ockham, a small village in Surrey. He is considered to be one of the major figures of medieval thought and was at the centre of the major intellectual and political controversies of...
:
The parts are actually there, in some sense. However, on this view, no infinite magnitude can have a number, for whatever number we can imagine, there is always a larger one: "There are not so many (in number) that there are no more." Aquinas
Thomas Aquinas
Thomas Aquinas, O.P. , also Thomas of Aquin or Aquino, was an Italian Dominican priest of the Catholic Church, and an immensely influential philosopher and theologian in the tradition of scholasticism, known as Doctor Angelicus, Doctor Communis, or Doctor Universalis...
also argued against the idea that infinity could be in any sense complete, or a totality.
Views from the Renaissance to modern times
GalileoGalileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
was the first to notice that we can place an infinite set into one-to-one correspondence with one of its proper subsets (any part of the set, that is not the whole). For example, we can match up the set of square number
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
s {1, 4, 9, 16, ...} with the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s {1, 2, 3, 4, ...} as follows:
- 1 → 1
2 → 4
3 → 9
4 → 16
…
It appeared, by this reasoning, as though a set which is naturally smaller than the set of which it is a part (since it does not contain all the members of that set) is in some sense the same "size". Galileo thought this was one of the difficulties which arise when we try, "with our finite minds," to comprehend the infinite.
The idea that size can be measured by one-to-one correspondence is today known as Hume's principle
Hume's principle
Hume's Principle or HP—the terms were coined by George Boolos—says that the number of Fs is equal to the number of Gs if and only if there is a one-to-one correspondence between the Fs and the Gs. HP can be stated formally in systems of second-order logic...
, although Hume, like Galileo, believed the principle could not be applied to infinite sets. (Mathematicians from the time of Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
do apply the principle to infinite sets, and do have a notion of some infinite quantities being greater than others.)
Locke
John Locke
John Locke FRS , widely known as the Father of Liberalism, was an English philosopher and physician regarded as one of the most influential of Enlightenment thinkers. Considered one of the first of the British empiricists, following the tradition of Francis Bacon, he is equally important to social...
, in common with most of the empiricist philosophers, also believed that we can have no proper idea of the infinite. They believed all our ideas were derived from sense data
Sense data
In the philosophy of perception, the theory of sense data was a popular view held the early 20th century by philosophers such as Bertrand Russell, C. D. Broad, H. H. Price, A.J. Ayer and G.E. Moore, among others. Sense data are supposedly mind-dependent objects whose existence and properties are...
or "impressions," and since all sensory impressions are inherently finite, so too are our thoughts and ideas. Our idea of infinity is merely negative or privative.
Famously, the ultra-empiricist Hobbes
Thomas Hobbes
Thomas Hobbes of Malmesbury , in some older texts Thomas Hobbs of Malmsbury, was an English philosopher, best known today for his work on political philosophy...
tried to defend the idea of a potential infinity in light of the discovery, by Evangelista Torricelli
Evangelista Torricelli
Evangelista Torricelli was an Italian physicist and mathematician, best known for his invention of the barometer.-Biography:Evangelista Torricelli was born in Faenza, part of the Papal States...
, of a figure (Gabriel's Horn
Gabriel's Horn
Gabriel's Horn is a geometric figure which has infinite surface area but encloses a finite volume. The name refers to the tradition identifying the Archangel Gabriel as the angel who blows the horn to announce Judgment Day, associating the divine, or infinite, with the finite...
) whose surface area
Surface area
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
is infinite, but whose volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
is finite. Not reported, this motivation of Hobbes came too late as curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s having infinite length yet bounding finite areas were known much before. Such seeming paradoxes are resolved by taking any finite figure and stretching its content infinitely in one direction; the magnitude of its content is unchanged as its divisions drop off geometrically but the magnitude of its bounds increases to infinity by necessity. Potentiality lies in the definitions of this operation, as well-defined
Well-defined
In mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...
and interconsistent mathematical axioms. A potential infinity is allowed by letting an infinitely-large quantity be cancelled out by an infinitely-small quantity.
Modern philosophical views
Modern discussion of the infinite is now regarded as part of set theory and mathematics. This discussion is generally avoided by philosophers. An exception was WittgensteinLudwig Wittgenstein
Ludwig Josef Johann Wittgenstein was an Austrian philosopher who worked primarily in logic, the philosophy of mathematics, the philosophy of mind, and the philosophy of language. He was professor in philosophy at the University of Cambridge from 1939 until 1947...
, who made an impassioned attack upon axiomatic set theory, and upon the idea of the actual infinite, during his "middle period".
Unlike the traditional empiricists, he thought that the infinite was in some way given to sense experience.
Ethics
The philosopher Emmanuel LevinasEmmanuel Lévinas
Emmanuel Levinas was a Lithuanian-born French Jewish philosopher and Talmudic commentator.-Life:Emanuelis Levinas received a traditional Jewish education in Lithuania...
uses infinity to designate that which cannot be defined or reduced to knowledge or power. In Levinas' magnum opus Totality and Infinity
Totality and Infinity
Totality and Infinity is a work of philosophy authored by Emmanuel Levinas. It advances the thesis that all ethics derive from a confrontation with an other...
he says,
Three types of infinities
Besides the mathematical infinity and the physical infinity, there could also be a philosophical infinity. There are scientists who hold that all three reallyPhilosophical realism
Contemporary philosophical realism is the belief that our reality, or some aspect of it, is ontologically independent of our conceptual schemes, linguistic practices, beliefs, etc....
exist and there are scientists who hold that none of the three exists. And in between there are the various possibilities. Rudy Rucker
Rudy Rucker
Rudolf von Bitter Rucker is an American mathematician, computer scientist, science fiction author, and philosopher, and is one of the founders of the cyberpunk literary movement. The author of both fiction and non-fiction, he is best known for the novels in the Ware Tetralogy, the first two of...
, in his book Infinity and the Mind — the Science and Philosophy of the Infinite (1982), has worked out a model list of representatives of each of the eight possible standpoints. The footnote on p. 335 of his book suggests the consideration of the following names: Abraham Robinson
Abraham Robinson
Abraham Robinson was a mathematician who is most widely known for development of non-standard analysis, a mathematically rigorous system whereby infinitesimal and infinite numbers were incorporated into mathematics....
, Plato
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
, Thomas Aquinas
Thomas Aquinas
Thomas Aquinas, O.P. , also Thomas of Aquin or Aquino, was an Italian Dominican priest of the Catholic Church, and an immensely influential philosopher and theologian in the tradition of scholasticism, known as Doctor Angelicus, Doctor Communis, or Doctor Universalis...
, L.E.J. Brouwer, David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
, Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
, Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
and Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
.
Structure of infinity, examples from metaphysics
- EternityEternityWhile in the popular mind, eternity often simply means existence for a limitless amount of time, many have used it to refer to a timeless existence altogether outside time. By contrast, infinite temporal existence is then called sempiternity. Something eternal exists outside time; by contrast,...
: linguistically the opposite of finite, having no edges, limits, an end: How deep is the sky? How can I write down the largest possible number? - Indefinite: How could God be sure that there is no-one greater?
- CircularityCircular definitionA circular definition is one that uses the term being defined as a part of the definition or assumes a prior understanding of the term being defined. Either the audience must already know the meaning of the key term, or the definition is deficient in including the term to be defined in the...
: The line defining a circle does not have an end. - RecursionRecursionRecursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
: See semantic satiation for instance. Lack of utter reason. Why is that? Apparently, a relevant question after any answer.
Other references
- D. P. AgrawalD. P. AgrawalProf. D. P. Agrawal is a Historian of Indian Science and Technology, archaeologist and author. He has published works on Indian archaeology, metallurgy, and history of science and Palaeoclimate.About the author...
(2000). Ancient Jaina Mathematics: an Introduction, Infinity Foundation. - L. C. Jain (1973). "Set theory in the Jaina school of mathematics", Indian Journal of History of Science.
- Ian Pearce (2002). 'Jainism', MacTutor History of Mathematics archiveMacTutor History of Mathematics archiveThe MacTutor History of Mathematics archive is a website maintained by John J. O'Connor and Edmund F. Robertson and hosted by the University of St Andrews in Scotland...
. - N. Singh (1988). 'Jaina Theory of Actual Infinity and Transfinite Numbers', Journal of Asiatic SocietyAsiatic SocietyThe Asiatic Society was founded by Sir William Jones on January 15, 1784 in a meeting presided over by Sir Robert Chambers, the Chief Justice of the Supreme Court at the Fort William in Calcutta, then capital of the British Raj, to enhance and further the cause of Oriental research. At the time of...
, Vol. 30.