Information gain in decision trees
Encyclopedia
In information theory
and machine learning
, information gain is an alternative synonym for Kullback–Leibler divergence
.
In particular, the information gain about a random variable X obtained from an observation that a random variable A takes the value A=a is the Kullback-Leibler divergence DKL( p(x|a) || p(x|I) ) of the prior distribution p(x|I) for x from the posterior distribution p(x|a) for x given a.
The expected value
of the information gain is the mutual information
I(X;A) of X and A — i.e. the reduction in the entropy
of X achieved by learning the state of the random variable A.
In machine learning this concept can be used to define a preferred sequence of attributes to investigate to most rapidly narrow down the state of X. Such a sequence (which depends on the outcome of the investigation of previous attributes at each stage) is called a decision tree
. Usually an attribute with high information gain should be preferred to other attributes.
from a prior state to a state that takes some information as given:
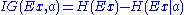
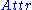be the set of all attributes and 
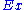the set of all training examples,
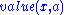with
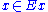defines the value of a specific example 
for attribute 
, 
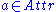specifies the entropy, and 
is the number of elements in the set 
.
The information gain for an attribute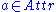
is defined as follows:
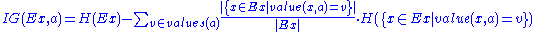
The information gain is equal to the total entropy for an attribute if for each of the attribute values a unique classification can be made for the result attribute. In this case the relative entropies subtracted from the total entropy are 0.
).
Information gain ratio
is sometimes used instead. This biases the decision tree against considering attributes with a large number of distinct values. However, attributes with very low information values then appeared to receive an unfair advantage. In addition, methods such as permutation tests have been proposed to correct the bias.
following way:
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
and machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
, information gain is an alternative synonym for Kullback–Leibler divergence
Kullback–Leibler divergence
In probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
.
In particular, the information gain about a random variable X obtained from an observation that a random variable A takes the value A=a is the Kullback-Leibler divergence DKL( p(x|a) || p(x|I) ) of the prior distribution p(x|I) for x from the posterior distribution p(x|a) for x given a.
The expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the information gain is the mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
I(X;A) of X and A — i.e. the reduction in the entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
of X achieved by learning the state of the random variable A.
In machine learning this concept can be used to define a preferred sequence of attributes to investigate to most rapidly narrow down the state of X. Such a sequence (which depends on the outcome of the investigation of previous attributes at each stage) is called a decision tree
Decision tree learning
Decision tree learning, used in statistics, data mining and machine learning, uses a decision tree as a predictive model which maps observations about an item to conclusions about the item's target value. More descriptive names for such tree models are classification trees or regression trees...
. Usually an attribute with high information gain should be preferred to other attributes.
General definition
In general terms, the expected information gain is the change in information entropyInformation entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
from a prior state to a state that takes some information as given:
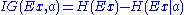
Formal definition
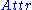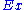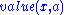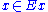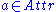Let be the set of all attributes and the set of all training examples, with defines the value of a specific example for attribute , specifies the entropy, and is the number of elements in the set .The information gain for an attribute
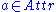is defined as follows: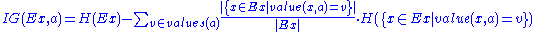The information gain is equal to the total entropy for an attribute if for each of the attribute values a unique classification can be made for the result attribute. In this case the relative entropies subtracted from the total entropy are 0.
Drawbacks
Although information gain is usually a good measure for deciding the relevance of an attribute, it is not perfect. A notable problem occurs when information gain is applied to attributes that can take on a large number of distinct values. For example, suppose that we are building a decision tree for some data describing the customers of a business. Information gain is often used to decide which of the attributes are the most relevant, so they can be tested near the root of the tree. One of the input attributes might be the customer's credit card number. This attribute has a high information gain, because it uniquely identifies each customer, but we do not want to include it in the decision tree: deciding how to treat a customer based on their credit card number is unlikely to generalize to customers we haven't seen before (overfittingOverfitting
In statistics, overfitting occurs when a statistical model describes random error or noise instead of the underlying relationship. Overfitting generally occurs when a model is excessively complex, such as having too many parameters relative to the number of observations...
).
Information gain ratio
Information gain ratio
- Information Gain Calculation :Let Attr be the set of all attributes and Ex the set of all training examples,value withx\in Ex defines the value of a specific example x for attribute a\in Attr, H specifies the entropy....
is sometimes used instead. This biases the decision tree against considering attributes with a large number of distinct values. However, attributes with very low information values then appeared to receive an unfair advantage. In addition, methods such as permutation tests have been proposed to correct the bias.
Constructing a decision tree using information gain
A decision tree can be constructed top-down using the information gain in thefollowing way:
- begin at the root node
- determine the attribute with the highest information gain which is not already used as an ancestor node
- add a child node for each possible value of that attribute
- attach all examples to the child node where the attribute values of the examples are identical to the attribute value attached to the node
- if all examples attached to the child node can be classified uniquely add that classification to that node and mark it as leaf node
- go back to step two if there are unused attributes left, otherwise add the classification of most of the examples attached to the child node