Infraparticle
Encyclopedia
An infraparticle is an electrically charged particle and its surrounding cloud of soft photons—of which there are infinite number, by virtue of the infrared divergence
of quantum electrodynamics
. That is, it is a dressed particle
rather than a bare particle
. Whenever electric charges accelerate they emit Bremsstrahlung radiation, whereby an infinite number of the virtual
soft photons become real particles. However, only a finite number of these photons are detectable, the remainder falling below the measurement threshold.
The form of the electric field at infinity, which is determined by the velocity of a point charge, defines superselection sectors for the particle's Hilbert space
. This is unlike the usual Fock space
description, where the Hilbert space includes particle states with different velocities.
Because of their infraparticle properties, charged particles do not have a sharp delta function
density of states like an ordinary particle, but instead the density of states rises like an inverse power at the mass of the particle. This collection of states which are very close in mass to m consist of the particle together with low-energy excitation of the electromagnetic field.
, in addition to the global
U(1)
symmetry related to the electric charge
, there are also position dependent gauge transformations. Noether's theorem
states that for every infinitesimal symmetry transformation that is local (local in the sense that the transformed value of a field at a given point only depends on the field configuration in an arbitrarily small neighborhood of that point), there is a corresponding conserved charge called the Noether charge, which is the space integral of a Noether density (assuming the integral converges and there is a Noether current satisfying the continuity equation
).
If this is applied to the global U(1) symmetry, the result
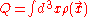(over all of space)
is the conserved charge where ρ is the charge density
. As long as the surface integral
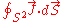
at the boundary at spatial infinity is zero, which is satisfied if the current density
J falls off sufficiently fast, the quantity Q is conserved. This is nothing other than the familiar electric charge.
But what if there is a position-dependent (but not time-dependent) infinitesimal gauge transformation
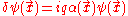where α is some function of position?
The Noether charge is now
where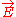
is the electric field
.
Using integration by parts
,
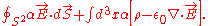
This assumes that the state in question approaches the vacuum asymptotically at spatial infinity. The first integral is the surface integral at spatial infinity and the second integral is zero by the Gauss law. Also assume that α(r,θ,φ) approaches α(θ,φ) as r approaches infinity (in polar coordinates). Then, the Noether charge only depends upon the value of α at spatial infinity but not upon the value of α at finite values. This is consistent with the idea that symmetry transformations not affecting the boundaries are gauge symmetries whereas those that do are global symmetries. If α(θ,φ) = 1 all over the S2, we get the electric charge. But for other functions, we also get conserved charges (which are not so well known).
This conclusion holds both in classical electrodynamics as well as in quantum electrodynamics. If α is taken as the spherical harmonics
, conserved scalar charges (the electric charge) are seen as well as conserved vector charges and conserved tensor charges. This is not a violation of the Coleman–Mandula theorem as there is no mass gap
. In particular, for each direction (a fixed θ and φ), the quantity
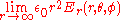
is a c-number
and a conserved quantity. Using the result that states with different charges exist in different superselection sector
s, the conclusion that states with the same electric charge but different values for the directional charges lie in different superselection sectors.
Even though this result is expressed in terms of a particular spherical coordinates with a given origin
, translations changing the origin do not affect spatial infinity.
s). The conclusion is that both electrons lie in different superselection sectors no matter how tiny the velocity is. At first sight, this might appear to be in contradiction with Wigner's classification
, which implies that the whole one-particle Hilbert space
lies in a single superselection sector, but it is not because m is really the greatest lower bound of a continuous mass spectrum and eigenstates of m only exist in a rigged Hilbert space
. The electron, and other particles like it is called an infraparticle.
The existence of the directional charges is related to soft photons. The directional charge at
and 
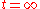are the same if we take the limit as r goes to infinity first and only then take the limit as t approaches infinity. If we interchange the limits, the directional charges change. This is related to the expanding electromagnetic waves spreading outwards at the speed of light (the soft photons).
More generally, there might exist a similar situation in other quantum field theories
besides QED. The name "infraparticle" still applies in those cases.
Infrared divergence
In physics, an infrared divergence or infrared catastrophe is a situation in which an integral, for example a Feynman diagram, diverges because of contributions of objects with very small energy approaching zero, or, equivalently, because of physical phenomena at very long distances.The infrared ...
of quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
. That is, it is a dressed particle
Dressed particle
In theoretical physics, the term dressed particle refers to a bare particle together with some excitations of other quantum fields that are physically inseparable from the bare particle...
rather than a bare particle
Bare particle
In theoretical physics, a bare particle is an excitation of an elementary quantum field. Such a particle is not identical to the particles observed in the experiments: the real particles are dressed particles that also include additional particles surrounding the bare one....
. Whenever electric charges accelerate they emit Bremsstrahlung radiation, whereby an infinite number of the virtual
Virtual particle
In physics, a virtual particle is a particle that exists for a limited time and space. The energy and momentum of a virtual particle are uncertain according to the uncertainty principle...
soft photons become real particles. However, only a finite number of these photons are detectable, the remainder falling below the measurement threshold.
The form of the electric field at infinity, which is determined by the velocity of a point charge, defines superselection sectors for the particle's Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. This is unlike the usual Fock space
Fock space
The Fock space is an algebraic system used in quantum mechanics to describe quantum states with a variable or unknown number of particles. It is named after V. A...
description, where the Hilbert space includes particle states with different velocities.
Because of their infraparticle properties, charged particles do not have a sharp delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
density of states like an ordinary particle, but instead the density of states rises like an inverse power at the mass of the particle. This collection of states which are very close in mass to m consist of the particle together with low-energy excitation of the electromagnetic field.
Noether's theorem for gauge transformations
In electrodynamics and quantum electrodynamicsQuantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
, in addition to the global
Global symmetry
A global symmetry is a symmetry that holds at all points in the spacetime under consideration, as opposed to a local symmetry which varies from point to point.Global symmetries require conservation laws, but not forces, in physics.-See also:...
U(1)
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
symmetry related to the electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
, there are also position dependent gauge transformations. Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
states that for every infinitesimal symmetry transformation that is local (local in the sense that the transformed value of a field at a given point only depends on the field configuration in an arbitrarily small neighborhood of that point), there is a corresponding conserved charge called the Noether charge, which is the space integral of a Noether density (assuming the integral converges and there is a Noether current satisfying the continuity equation
Continuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
).
If this is applied to the global U(1) symmetry, the result
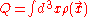(over all of space)is the conserved charge where ρ is the charge density
Charge density
The linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
. As long as the surface integral
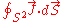
at the boundary at spatial infinity is zero, which is satisfied if the current density
Current density
Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
J falls off sufficiently fast, the quantity Q is conserved. This is nothing other than the familiar electric charge.
But what if there is a position-dependent (but not time-dependent) infinitesimal gauge transformation
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
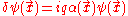where α is some function of position? The Noether charge is now
where
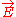is the electric fieldElectric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
.
Using integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
,
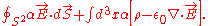
This assumes that the state in question approaches the vacuum asymptotically at spatial infinity. The first integral is the surface integral at spatial infinity and the second integral is zero by the Gauss law. Also assume that α(r,θ,φ) approaches α(θ,φ) as r approaches infinity (in polar coordinates). Then, the Noether charge only depends upon the value of α at spatial infinity but not upon the value of α at finite values. This is consistent with the idea that symmetry transformations not affecting the boundaries are gauge symmetries whereas those that do are global symmetries. If α(θ,φ) = 1 all over the S2, we get the electric charge. But for other functions, we also get conserved charges (which are not so well known).
This conclusion holds both in classical electrodynamics as well as in quantum electrodynamics. If α is taken as the spherical harmonics
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
, conserved scalar charges (the electric charge) are seen as well as conserved vector charges and conserved tensor charges. This is not a violation of the Coleman–Mandula theorem as there is no mass gap
Mass gap
In quantum field theory, the mass gap is the difference in energy between the vacuum and the next lowest energy state. The energy of the vacuum is zero by definition, and assuming that all energy states can be thought of as particles in plane-waves, the mass gap is the mass of the lightest...
. In particular, for each direction (a fixed θ and φ), the quantity
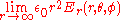
is a c-number
C-number
The term c-number is an old nomenclature used by Paul Dirac which refers to real and complex numbers. It is used to distinguish from operators in quantum mechanics....
and a conserved quantity. Using the result that states with different charges exist in different superselection sector
Superselection sector
In Quantum mechanics, superselection extends the concept of selection rules.Superselection rules are postulated rules forbidding the preparation of quantum states that exhibit coherence between eigenstates of certain observables....
s, the conclusion that states with the same electric charge but different values for the directional charges lie in different superselection sectors.
Even though this result is expressed in terms of a particular spherical coordinates with a given origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
, translations changing the origin do not affect spatial infinity.
Implication for particle behavior
The directional charges are different for an electron that has always been at rest and an electron that has always been moving at a certain nonzero velocity (because of the Lorentz transformationLorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s). The conclusion is that both electrons lie in different superselection sectors no matter how tiny the velocity is. At first sight, this might appear to be in contradiction with Wigner's classification
Wigner's classification
In mathematics and theoretical physics, Wigner's classificationis a classification of the nonnegative energy irreducible unitary representations of the Poincaré group, which have sharp mass eigenvalues...
, which implies that the whole one-particle Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
lies in a single superselection sector, but it is not because m is really the greatest lower bound of a continuous mass spectrum and eigenstates of m only exist in a rigged Hilbert space
Rigged Hilbert space
In mathematics, a rigged Hilbert space is a construction designed to link the distribution and square-integrable aspects of functional analysis. Such spaces were introduced to study spectral theory in the broad sense...
. The electron, and other particles like it is called an infraparticle.
The existence of the directional charges is related to soft photons. The directional charge at
and 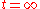are the same if we take the limit as r goes to infinity first and only then take the limit as t approaches infinity. If we interchange the limits, the directional charges change. This is related to the expanding electromagnetic waves spreading outwards at the speed of light (the soft photons).More generally, there might exist a similar situation in other quantum field theories
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
besides QED. The name "infraparticle" still applies in those cases.