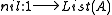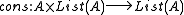Initial algebra
Encyclopedia
In mathematics
, an initial algebra is an initial object
in the category of F-algebras
for a given endofunctor F. The initiality provides a general framework for induction
and recursion
.
For instance, consider the endofunctor 1+(-) on the category of sets, where 1 is the one-point set, the terminal object in the category. An algebra for this endofunctor is a set X (called the carrier of the algebra) together with a point and a function . The set of natural number
s is the carrier of the initial such algebra: the point is zero and the function is the successor map.
For a second example, consider the endofunctor 1+N×(-) on the category of sets, where N is the set of natural numbers. An algebra for this endofunctor is a set X together with a point and a function . The set of finite lists of natural numbers is the initial such algebra. The point is the empty list, and the function is cons
, taking a number and a finite list, and returning a new finite list with the number at the head.
. The finality provides a general framework for coinduction
and corecursion
.
For example, using the same functor 1+(-) as before, a coalgebra is a set X together with a truth-valued test function and a partial function
whose domain is formed by those for which . The set } consisting of the natural numbers extended with a new element ω is the carrier of the final coalgebra in the category, where p is the test for zero: , ; and f is the predecessor function (the inverse
of the successor function) on the positive naturals, but acts like the identity
on the new element ω: , .
For a second example, consider the same functor 1+N×(-) as before. In this case the carrier of the final coalgebra consists of all lists of natural numbers, finite as well as infinite. The operations are a test function testing whether a list is empty, and a deconstruction function defined on nonempty lists returning a pair consisting of the head and the tail of the input list.
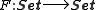sending 
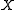to 
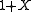. Then the set 
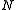of natural number
s together with the functions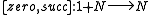
, where 
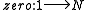and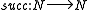 
are the obvious functions suggested by their names, is an initial 
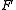-algebra. The initiality (the universal property
for this case) is not hard to establish; the unique homomorphism
to an arbitrary F-algebra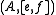
, for 
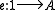an element of A and 
a function
on A, is the function sending the natural number n to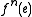
, that is, 
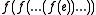, the n-fold application of f to e.
s, can be obtained as initial algebras of specific endofunctors.
While there may be several initial algebras for a given endofunctor, they are unique up to
isomorphism
, which informally means that the "observable" properties of a data structure can be adequately captured by defining it as an initial algebra.
To obtain the type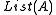
of lists whose elements are members of set A, consider that the list-forming operations are:
Combined into one function, they give:
which makes this an F-algebra for the endofunctor F sending
to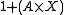 
. It is, in fact, the initial F-algebra. Initiality is established by the function known as foldr
in functional
programming language
s such as Haskell
and ML
.
Likewise, binary tree
s with elements at the leaves can be obtained as the initial algebra
Types obtained this way are known as algebraic data type
s.
Types defined by using least fixed point
construct with functor F can be regarded as an initial F-algebra
, provided that parametricity
holds for the type.
In a dual
way, similar relationship exists between notions of greatest fixed point and terminal F-coalgebra
, with applications to coinductive types. These can be used for allowing potentially infinite
objects while maintaining strong normalization property
. In the strongly normalizing Charity programming language (i.e. each program terminates), coinductive data types can be used achieving surprising results, e.g. defining lookup
constructs to implement such “strong”
functions like the Ackermann function
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an initial algebra is an initial object
Initial object
In category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
in the category of F-algebras
F-algebra
In mathematics, specifically in category theory, an F-algebra is a structure defined according to a functor F. F-algebras can be used to represent data structures used in programming, such as lists and trees...
for a given endofunctor F. The initiality provides a general framework for induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
and recursion
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
.
For instance, consider the endofunctor 1+(-) on the category of sets, where 1 is the one-point set, the terminal object in the category. An algebra for this endofunctor is a set X (called the carrier of the algebra) together with a point and a function . The set of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s is the carrier of the initial such algebra: the point is zero and the function is the successor map.
For a second example, consider the endofunctor 1+N×(-) on the category of sets, where N is the set of natural numbers. An algebra for this endofunctor is a set X together with a point and a function . The set of finite lists of natural numbers is the initial such algebra. The point is the empty list, and the function is cons
Cons
In computer programming, cons is a fundamental function in most dialects of the Lisp programming language. cons constructs memory objects which hold two values or pointers to values. These objects are referred to as cells, conses, non-atomic s-expressions , or pairs...
, taking a number and a finite list, and returning a new finite list with the number at the head.
Final coalgebra
Dually, a final coalgebra is a terminal object in the category of F-coalgebrasF-coalgebra
In mathematics, specifically in category theory, an F-coalgebra is a structure defined according to a functor F. For both algebra and coalgebra, a functor is a convenient and general way of organizing a signature...
. The finality provides a general framework for coinduction
Coinduction
In computer science, coinduction is a technique for defining and proving properties of systems of concurrent interacting objects.Coinduction is the mathematical dual to structural induction...
and corecursion
Corecursion
In computer science, corecursion is a type of operation that is dual to recursion. Corecursion and codata allow total languages to work with infinite data structures such as streams. Corecursion is often used in conjunction with lazy evaluation. Corecursion can produce both finite and infinite data...
.
For example, using the same functor 1+(-) as before, a coalgebra is a set X together with a truth-valued test function and a partial function
Partial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
whose domain is formed by those for which . The set } consisting of the natural numbers extended with a new element ω is the carrier of the final coalgebra in the category, where p is the test for zero: , ; and f is the predecessor function (the inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of the successor function) on the positive naturals, but acts like the identity
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on the new element ω: , .
For a second example, consider the same functor 1+N×(-) as before. In this case the carrier of the final coalgebra consists of all lists of natural numbers, finite as well as infinite. The operations are a test function testing whether a list is empty, and a deconstruction function defined on nonempty lists returning a pair consisting of the head and the tail of the input list.
Theorems
- Initial algebras are minimal (i.e., have no proper subalgebra)
- Final coalgebras are simple (i.e., have no proper quotients).
Example
Consider the endofunctor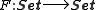 sending 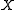to 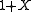. Then the set 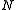of natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s together with the functions
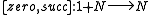, where 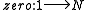and 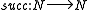are the obvious functions suggested by their names, is an initial 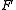-algebra. The initiality (the universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
for this case) is not hard to establish; the unique homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
to an arbitrary F-algebra
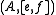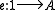, for an element of A and a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on A, is the function sending the natural number n to
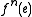, that is, 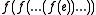, the n-fold application of f to e.Use in Computer Science
Various finite data structures used in programming, such as lists and treeTree
A tree is a perennial woody plant. It is most often defined as a woody plant that has many secondary branches supported clear of the ground on a single main stem or trunk with clear apical dominance. A minimum height specification at maturity is cited by some authors, varying from 3 m to...
s, can be obtained as initial algebras of specific endofunctors.
While there may be several initial algebras for a given endofunctor, they are unique up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
, which informally means that the "observable" properties of a data structure can be adequately captured by defining it as an initial algebra.
To obtain the type
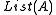of lists whose elements are members of set A, consider that the list-forming operations are:
Combined into one function, they give:
,
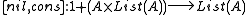which makes this an F-algebra for the endofunctor F sending
to 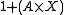. It is, in fact, the initial F-algebra. Initiality is established by the function known as foldrFold (higher-order function)
In functional programming, fold – also known variously as reduce, accumulate, compress, or inject – are a family of higher-order functions that analyze a recursive data structure and recombine through use of a given combining operation the results of recursively processing its...
in functional
Functional programming
In computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It emphasizes the application of functions, in contrast to the imperative programming style, which emphasizes changes in state...
programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s such as Haskell
Haskell (programming language)
Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
and ML
ML programming language
ML is a general-purpose functional programming language developed by Robin Milner and others in the early 1970s at the University of Edinburgh, whose syntax is inspired by ISWIM...
.
Likewise, binary tree
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
s with elements at the leaves can be obtained as the initial algebra
.
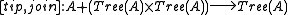Types obtained this way are known as algebraic data type
Algebraic data type
In computer programming, particularly functional programming and type theory, an algebraic data type is a datatype each of whose values is data from other datatypes wrapped in one of the constructors of the datatype. Any wrapped datum is an argument to the constructor...
s.
Types defined by using least fixed point
Least fixed point
In order theory, a branch of mathematics, the least fixed point of a function is the fixed point which is less than or equal to all other fixed points, according to some partial order....
construct with functor F can be regarded as an initial F-algebra
F-algebra
In mathematics, specifically in category theory, an F-algebra is a structure defined according to a functor F. F-algebras can be used to represent data structures used in programming, such as lists and trees...
, provided that parametricity
Parametricity
Parametricity is a result in the theory of programming languages in computer science. The principle of parametricity dictates that functions with similar types have similar properties.- Theory of parametricity :...
holds for the type.
In a dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
way, similar relationship exists between notions of greatest fixed point and terminal F-coalgebra
F-coalgebra
In mathematics, specifically in category theory, an F-coalgebra is a structure defined according to a functor F. For both algebra and coalgebra, a functor is a convenient and general way of organizing a signature...
, with applications to coinductive types. These can be used for allowing potentially infinite
Actual infinity
Actual infinity is the idea that numbers, or some other type of mathematical object, can form an actual, completed totality; namely, a set. Hence, in the philosophy of mathematics, the abstraction of actual infinity involves the acceptance of infinite entities, such as the set of all natural...
objects while maintaining strong normalization property
Normalization property (lambda-calculus)
In mathematical logic and theoretical computer science, a rewrite system has the strong normalization property if every term is strongly normalizing; that is, if every sequence of rewrites eventually terminates to a term in normal form...
. In the strongly normalizing Charity programming language (i.e. each program terminates), coinductive data types can be used achieving surprising results, e.g. defining lookup
Lookup table
In computer science, a lookup table is a data structure, usually an array or associative array, often used to replace a runtime computation with a simpler array indexing operation. The savings in terms of processing time can be significant, since retrieving a value from memory is often faster than...
constructs to implement such “strong”
Computability theory (computer science)
Computability is the ability to solve a problem in an effective manner. It is a key topic of the field of computability theory within mathematical logic and the theory of computation within computer science...
functions like the Ackermann function
Ackermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
.
External links
- Categorical programming with inductive and coinductive types by Varmo Vene
- Philip Wadler: Recursive types for free! University of Glasgow, July 1998. Draft.
- Initial Algebra and Final Coalgebra Semantics for Concurrency by J.J.M.M. Rutten and D. Turi
- Initiality and finality from CLiki