
Integer circuit
Encyclopedia
Integer
circuit
s is a mathematical model used in studying computational complexity theory
. It is a special case of circuit
, the object is a labeled directed acyclic graph
the nodes of which evaluate to sets of integers, the leaves are finite sets, and the gates are set operations or arithmetic operations.
As an algorithm
ic problem, the possible questions are to find if a given integer is an element of the output node or if two circuits compute the same set. The decidability is still an open question, but there are results on restriction of thoses circuits. Finding answers to some questions about this model could serve as a proof to many important mathematical conjectures, like Goldbach's conjecture
.
It is a natural extension of the circuits over sets of natural numbers
when the considered set contains also negative integers, the definitions, which does not change, will not be repeated on this page. Only the differences will be mentioned.
 and a circuit, if
and a circuit, if  is in the output gate of the circuit.
is in the output gate of the circuit.
When the class of authorized gate is restricted, the membership problem lay inside well kwown complexity classes.
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
circuit
Circuit (computer theory)
A circuit in computer theory is a theoretical structure simulating electrical and data paths, in which voltage and binary values enter at the beginning of the circuit, go through gates which do some computation and output an answer. An important special case of circuits is the boolean...
s is a mathematical model used in studying computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
. It is a special case of circuit
Circuit (computer theory)
A circuit in computer theory is a theoretical structure simulating electrical and data paths, in which voltage and binary values enter at the beginning of the circuit, go through gates which do some computation and output an answer. An important special case of circuits is the boolean...
, the object is a labeled directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
the nodes of which evaluate to sets of integers, the leaves are finite sets, and the gates are set operations or arithmetic operations.
As an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
ic problem, the possible questions are to find if a given integer is an element of the output node or if two circuits compute the same set. The decidability is still an open question, but there are results on restriction of thoses circuits. Finding answers to some questions about this model could serve as a proof to many important mathematical conjectures, like Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
.
It is a natural extension of the circuits over sets of natural numbers
Circuits over sets of natural numbers
Circuits over natural numbers is a mathematical model used in studying computational complexity theory. It is a special case of circuit, the object is a labeled directed acyclic graph the nodes of which evaluate to sets of natural numbers, the leaves are finite sets, and the gates are set...
when the considered set contains also negative integers, the definitions, which does not change, will not be repeated on this page. Only the differences will be mentioned.
Membership problem
The membership problem ask if, given an element and a circuit, if
and a circuit, if  is in the output gate of the circuit.
is in the output gate of the circuit.When the class of authorized gate is restricted, the membership problem lay inside well kwown complexity classes.
| O | MC (O) (O) |
MF (O) (O) |
|---|---|---|
| ∪,∩,−,+,× | NEXPTIME NEXPTIME In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O for some polynomial p, and unlimited space.... -hard |
PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -hard |
| ∪,∩,+,× | NEXPTIME NEXPTIME In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O for some polynomial p, and unlimited space.... -complete |
NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
| ∪,+,× | NEXPTIME NEXPTIME In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O for some polynomial p, and unlimited space.... -complete |
NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
| ∩,+,× | P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... -hard, in co-NP |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -hard, in LOGCFL LOGCFL In computational complexity theory, LOGCFL is the complexity class that contains all decision problems that can be reduced in logarithmic space to a context-free language. This class is situated between NL and AC1, in the sense that it contains the former and is contained in the latter... |
| +,× | P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... -hard, in co-NP |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -hard, in LOGCFL LOGCFL In computational complexity theory, LOGCFL is the complexity class that contains all decision problems that can be reduced in logarithmic space to a context-free language. This class is situated between NL and AC1, in the sense that it contains the former and is contained in the latter... |
| ∪,∩,−,+ | PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
| ∪,∩,+ | PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
| ∪,+ | NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
| ∩,+ | C=L-complete | L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| + | C=L-complete | L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| ∪,∩,−,× | PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
| ∪,∩,× | PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
| ∪,× | NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
| ∩,× | (C=L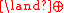 L)-hard, in P L)-hard, in PP (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| × | (NL NL (complexity) In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space.... -complete 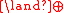 L)-complete L)-complete |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| ∪,∩,− | P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... -complete |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| ∪,∩ | P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... -complete |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| ∪ | NL NL (complexity) In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space.... -complete |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| ∩ | NL NL (complexity) In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space.... -complete |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |

