Circuits over sets of natural numbers
Encyclopedia
Circuit
s over natural number
s is a mathematical model used in studying computational complexity theory
. It is a special case of circuit
, the object is a labeled directed acyclic graph
the nodes of which evaluate to sets of natural numbers, the leaves are finite sets, and the gates are set operations or arithmetic operations.
As an algorithm
ic problem, the possible question are to find if a given natural number is an element is in the output node or if two circuits compute the same set. The decidability is still an open question, but there are results on restriction of those circuits. Finding answers to some questions about this model could serve as a proof to many important mathematical conjectures, like Goldbach's conjecture
.
, i.e. a labelled directed acyclic graph
of in-degree at most 2. The nodes of in-degree 0, the leaves, are finite sets of natural numbers, the labels of the nodes of in-degree 1 are −, where
and the labels of the nodes of in-degree 2 are +, × and ∪, where 
, 
and ∪ and ∩ with the usual set meaning.
The subset of circuits which do not use all of the possible labels are also studied.
For circuits which use all the labels, all these problems are equivalent.
They are all equivalent if we can use any labels for the gates.
The first problem is reducible to the third one, by asking if the node n is a subset of the output node.
The second problem is reducible to the first one, it suffices to multiply the output gate by 0, then 0 will be in the output gate if and only if the former output gate were not empty.
The third problem is reducible to the second one, checking if A is a subset of B is equivalent to ask if there is an element in
.
.
Goldbach's conjecture
asks if there is an even number greater than 2 which is not the sum of two prime numbers, it is natural to rephrase this question by asking if there is an element in
.
, then one can easily prove by induction on 
that 
, indeed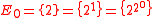 
and by induction 
.
And even double exponential—sized sets: let
, then 
, i.e. 
contains the 
firsts number. Once again this can be proved by induction on 
, it is true for 
by definition and let 
, dividing 
by 
we see it can be written as 
where 
, and by induction, 
and 
are in 
, so indeed 
.
Those examples explains why addition and multiplication are enough to create problem of high complexity.
When the class of authorized gate is restricted, the membership problem lay inside well known complexity classes.
When the class of authorized gate is restricted, the equivalence problem lay inside well known complexity classes. We call EC(O) and EF(O) the problem of equivalence over circuits and formulae the gate of which are in O.
Circuit (computer theory)
A circuit in computer theory is a theoretical structure simulating electrical and data paths, in which voltage and binary values enter at the beginning of the circuit, go through gates which do some computation and output an answer. An important special case of circuits is the boolean...
s over natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s is a mathematical model used in studying computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
. It is a special case of circuit
Circuit (computer theory)
A circuit in computer theory is a theoretical structure simulating electrical and data paths, in which voltage and binary values enter at the beginning of the circuit, go through gates which do some computation and output an answer. An important special case of circuits is the boolean...
, the object is a labeled directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
the nodes of which evaluate to sets of natural numbers, the leaves are finite sets, and the gates are set operations or arithmetic operations.
As an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
ic problem, the possible question are to find if a given natural number is an element is in the output node or if two circuits compute the same set. The decidability is still an open question, but there are results on restriction of those circuits. Finding answers to some questions about this model could serve as a proof to many important mathematical conjectures, like Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
.
Formal definition
An natural number circuit is a circuitCircuit complexity
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of Boolean circuits that compute them....
, i.e. a labelled directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
of in-degree at most 2. The nodes of in-degree 0, the leaves, are finite sets of natural numbers, the labels of the nodes of in-degree 1 are −, where
and the labels of the nodes of in-degree 2 are +, × and ∪, where , and ∪ and ∩ with the usual set meaning.The subset of circuits which do not use all of the possible labels are also studied.
Algorithmic problems
One can ask:- Is a given number n a member of the output node.
- Is the output node empty, does it contain a specific element, is it equal to
? - Is one node is a subset of another.
For circuits which use all the labels, all these problems are equivalent.
They are all equivalent if we can use any labels for the gates.
Proof
The first problem is reducible to the second one, by taking the intersection of the output gate and n. Indeed the new output get will be empty if and only if n was not an element of the former output gate.The first problem is reducible to the third one, by asking if the node n is a subset of the output node.
The second problem is reducible to the first one, it suffices to multiply the output gate by 0, then 0 will be in the output gate if and only if the former output gate were not empty.
The third problem is reducible to the second one, checking if A is a subset of B is equivalent to ask if there is an element in
.Restrictions
Let O be a subset of {∪,∩,−,+,×}, then we call MC(O) the problem of finding if a natural number is inside the output gate of a circuit the gates' labels of which are in O, and MF(O) the same problem with the added constraint that the circuit must be a treeTree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
.
Examples
- The set of numbers greater than n is
. In particular 
? - The set of prime numbers with 0 and 1, PRIME' is the complement of the numbers who are multiple of 2 natural numbers greater than 2, so it is
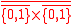
- The set of prime numbers, PRIME is then PRIME'
, the elements of PRIME' greater than 2. - The set of EVEN numbers is
.
Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
asks if there is an even number greater than 2 which is not the sum of two prime numbers, it is natural to rephrase this question by asking if there is an element in
.Quickly growing set
One difficulty come from the fact that the complement of a finite set is infinite, and computer has got only a finite memory. But even without complementation, one can create double exponential number. Let, then one can easily prove by induction on that , indeed 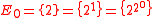and by induction .And even double exponential—sized sets: let
, then , i.e. contains the firsts number. Once again this can be proved by induction on , it is true for by definition and let , dividing by we see it can be written as where , and by induction, and are in , so indeed .Those examples explains why addition and multiplication are enough to create problem of high complexity.
Membership problem
The membership problem ask if, given an element n and a circuit, if n is in the output gate of the circuit.When the class of authorized gate is restricted, the membership problem lay inside well known complexity classes.
| O | MC(O) | MF(O) |
|---|---|---|
| ∪,∩,−,+,× | NEXPTIME NEXPTIME In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O for some polynomial p, and unlimited space.... -hard Decidable with an oracle Oracle machine In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any... for the halting problem Halting problem In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever... |
PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -hard |
| ∪,∩,+,× | NEXPTIME NEXPTIME In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O for some polynomial p, and unlimited space.... -complete |
NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
| ∪,+,× | PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
| ∩,+,× | P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... -hard, in co-R |
LOGCFL LOGCFL In computational complexity theory, LOGCFL is the complexity class that contains all decision problems that can be reduced in logarithmic space to a context-free language. This class is situated between NL and AC1, in the sense that it contains the former and is contained in the latter... |
| +,× | P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... -complete |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| ∪,∩,−,+ | PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
| ∪,∩,+ | PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
| ∪,+ | NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
| ∩,+ | C=L-complete | L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| + | C=L-complete | L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| ∪,∩,−,× | PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
| ∪,∩,× | PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
| ∪,× | NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard... |
| ∩,× | C=L-hard, in P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| × | NL NL (complexity) In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space.... -complete |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| ∪,∩,− | P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... -complete |
NC1 NC (complexity) In complexity theory, the class NC is the set of decision problems decidable in polylogarithmic time on a parallel computer with a polynomial number of processors. In other words, a problem is in NC if there exist constants c and k such that it can be solved in time O using O parallel processors... -complete |
| ∪,∩ | P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... -complete |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| ∪ | NL NL (complexity) In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space.... -complete |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| ∩ | NL NL (complexity) In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space.... -complete |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
Equivalence problem
The equivalence problem ask if, given two gates of a circuits, they evaluate to the same set.When the class of authorized gate is restricted, the equivalence problem lay inside well known complexity classes. We call EC(O) and EF(O) the problem of equivalence over circuits and formulae the gate of which are in O.
| O | EC(O) | EF(O) |
|---|---|---|
| ∪,∩,−,+,× | NEXPTIME NEXPTIME In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O for some polynomial p, and unlimited space.... -hard Decidable with an oracle Oracle machine In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any... for the halting problem Halting problem In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever... |
PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -hard Decidable with an oracle Oracle machine In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any... for the halting problem Halting problem In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever... |
| ∪,∩,+,× | NEXPTIME NEXPTIME In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O for some polynomial p, and unlimited space.... -hard, in coNEXP NEXPTIME In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O for some polynomial p, and unlimited space.... NP NP (complexity) In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."... |
ΠP2 Polynomial hierarchy In computational complexity theory, the polynomial hierarchy is a hierarchy of complexity classes that generalize the classes P, NP and co-NP to oracle machines... -complete |
| ∪,+,× | NEXPTIME NEXPTIME In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O for some polynomial p, and unlimited space.... -hard, in coNEXP NEXPTIME In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O for some polynomial p, and unlimited space.... NP NP (complexity) In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."... |
ΠP2 Polynomial hierarchy In computational complexity theory, the polynomial hierarchy is a hierarchy of complexity classes that generalize the classes P, NP and co-NP to oracle machines... -complete |
| ∩,+,× | P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... -hard, in BPP |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -hard, in LOGCFL LOGCFL In computational complexity theory, LOGCFL is the complexity class that contains all decision problems that can be reduced in logarithmic space to a context-free language. This class is situated between NL and AC1, in the sense that it contains the former and is contained in the latter... |
| +,× | L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -hard, in LOGCFL LOGCFL In computational complexity theory, LOGCFL is the complexity class that contains all decision problems that can be reduced in logarithmic space to a context-free language. This class is situated between NL and AC1, in the sense that it contains the former and is contained in the latter... |
P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... -hard, in coRP RP (complexity) In complexity theory, RP is the complexity class of problems for which a probabilistic Turing machine exists with these properties:* It always runs in polynomial time in the input size... |
| ∪,∩,−,+ | PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
| ∪,∩,+ | PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
ΠP2 Polynomial hierarchy In computational complexity theory, the polynomial hierarchy is a hierarchy of complexity classes that generalize the classes P, NP and co-NP to oracle machines... -complete |
| ∪,+ | ΠP2 Polynomial hierarchy In computational complexity theory, the polynomial hierarchy is a hierarchy of complexity classes that generalize the classes P, NP and co-NP to oracle machines... -complete |
ΠP2 Polynomial hierarchy In computational complexity theory, the polynomial hierarchy is a hierarchy of complexity classes that generalize the classes P, NP and co-NP to oracle machines... -complete |
| ∩,+ | coC=L(2)-complete | L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| + | C=L-complete | L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| ∪,∩,−,× | PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
| ∪,∩,× | PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... -complete |
ΠP2 Polynomial hierarchy In computational complexity theory, the polynomial hierarchy is a hierarchy of complexity classes that generalize the classes P, NP and co-NP to oracle machines... -complete |
| ∪,× | ΠP2 Polynomial hierarchy In computational complexity theory, the polynomial hierarchy is a hierarchy of complexity classes that generalize the classes P, NP and co-NP to oracle machines... -complete |
ΠP2 Polynomial hierarchy In computational complexity theory, the polynomial hierarchy is a hierarchy of complexity classes that generalize the classes P, NP and co-NP to oracle machines... -complete |
| ∩,× | coC=L(2)-hard, in P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| × | C=L-hared, in P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| ∪,∩,− | P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... -complete |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| ∪,∩ | P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... -complete |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| ∪ | NL NL (complexity) In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space.... -complete |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
| ∩ | NL NL (complexity) In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space.... -complete |
L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... -complete |
External links
- Pierre McKenzie, The complexity of circuit evaluation over the natural numbers