Integration by reduction formulae
Encyclopedia
Integration by reduction formulae can be used when we want to integrate a function raised to the power n. If we have such an integral we can establish a reduction formula which can be used to calculate the integral for any value of n.
, integration by parts
, integration by trigonometric substitution
, integration by partial fractions, etc. The main idea is to express an integral involving a power of a function, represented by In, in terms of an integral that involves a lower power of that function, for example In-2. This makes reduction formulae a type of recurrence relation
. In other words, the reduction formulae express the integral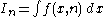
in terms of 
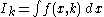, where 
.
This method of integration is one of the earliest used methods of integration.
Cosine integral
Typically, integrals like
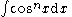
can be evaluated by a reduction formula.
Start by setting:
Now re-write as:
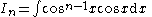
Integrating by this substitution:
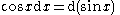
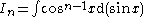
Now integrating by parts:
solving for In:
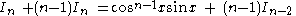
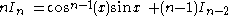
so the reduction formula is:
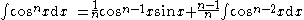
To supplement the example, the above can be used to evaluate the integral for (say) n = 5;
.
Calculating lower indices:
: 
: 
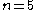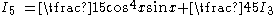
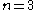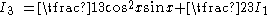
back-substituting:
，
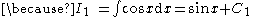
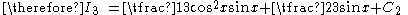, where C is a constant.
Exponential integral
Another typical example is:
.
Start by setting:
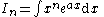
Integrating by substitution:
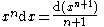
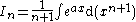
Now integrating by parts:
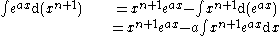
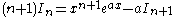
shifting indices back by 1 (so n + 1 → n, n → n – 1):
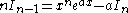
solving for n:
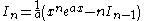
so the reduction formula is:
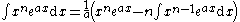
note that by the laws of indices
:
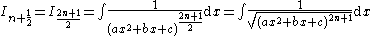
The following integrals contain:
.
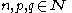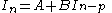
where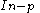
represents a shift of p integrals backwards relative to 
, and A and B are the collected extra terms (not constants), the general formulae for these integrals can be found by repeated back-substitution:
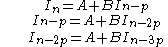
etc., so the general recurrence shift is:
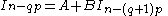
where q is a multiple of p. Performing back substitution to the index n - pq, carefully expanding brackets:
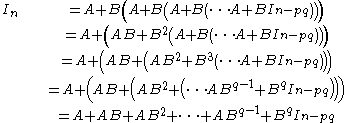
which leads to:
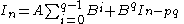
This can be used to obtain the integral as far back as pq indices relative to n, but it helps to transform indices to q, depending on the choice of p (it doesn't matter if n or q is the index). The transform is a simple substitution:
If I0 is known then we can set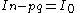
, then 
so 
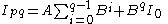
If I1 is known then we can set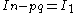
, then 
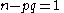so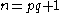 
Often, as can be seen in the tables above, p = 1 or p = 2, so the reduction formulae can be set up like so:
These can be used to short-cut the actual repeated use of the reduction formula.
can show the general formula
to hold 
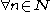. The proof can be split into two in the same way as above;
Case 1: one for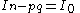
so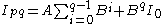 
Case 2: one for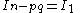
so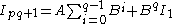 
For case 2 the index shift is +1, so the proof would be identical to case 1. Only case 1 is proved below.
Case 1:
It can be found that:
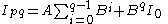
is true for q = 1;
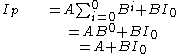
Now assume
is true for some q > 1, then show the formula holds for q + 1:
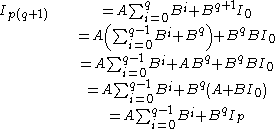
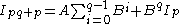
which corresponds to an index shift from I0 to Ip and Ipq to Ipq+p by +p. So the formula must be true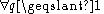
.
How to find the reduction formula
The reduction formula can be derived using any of the common methods of integration, like integration by substitutionIntegration by substitution
In calculus, integration by substitution is a method for finding antiderivatives and integrals. Using the fundamental theorem of calculus often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians...
, integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
, integration by trigonometric substitution
Trigonometric substitution
In mathematics, trigonometric substitution is the substitution of trigonometric functions for other expressions. One may use the trigonometric identities to simplify certain integrals containing radical expressions:...
, integration by partial fractions, etc. The main idea is to express an integral involving a power of a function, represented by In, in terms of an integral that involves a lower power of that function, for example In-2. This makes reduction formulae a type of recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
. In other words, the reduction formulae express the integral
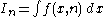in terms of 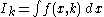, where .This method of integration is one of the earliest used methods of integration.
How to compute the integral
To compute the integral, we set n to its value and use the reduction formula to calculate the (n – 1) or (n – 2) integral. The higher index integral can be used to calculate lower index ones; the process is continued repeatedly until we reach a point where the function to be integrated can be computed, usually when it is to the index 0 or 1. Then we back-substitute the previous results until we have computed In.Examples
Below are examples to exemplify the procedure.Cosine integral
Typically, integrals like
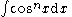
can be evaluated by a reduction formula.
Now re-write as:
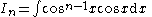
Integrating by this substitution:
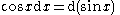
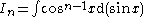
Now integrating by parts:
solving for In:
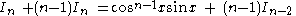
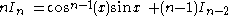
so the reduction formula is:
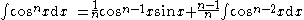
To supplement the example, the above can be used to evaluate the integral for (say) n = 5;
.Calculating lower indices:
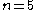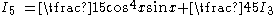
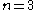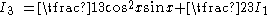
: : back-substituting:
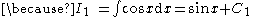
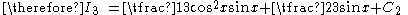，, where C is a constant.Exponential integral
Another typical example is:
.Start by setting:
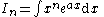
Integrating by substitution:
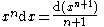
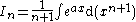
Now integrating by parts:
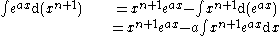
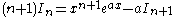
shifting indices back by 1 (so n + 1 → n, n → n – 1):
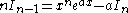
solving for n:
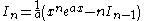
so the reduction formula is:
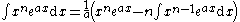
Rational functions
The following integrals contain:- Factors of the linearLinear equationA linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
radicalSquare rootIn mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
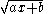
- Linear factors
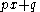and the linear radical 
- QuadraticQuadraticIn mathematics, the term quadratic describes something that pertains to squares, to the operation of squaring, to terms of the second degree, or equations or formulas that involve such terms...
factors
- Quadratic factors
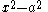, for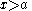 
- Quadratic factors
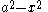, for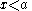 
- (IrreducibleIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
) quadratic factors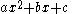
- Radicals of irreducible quadratic factors
| Integral | Reduction formula |
|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
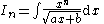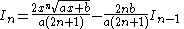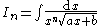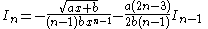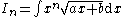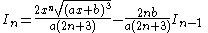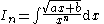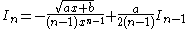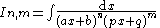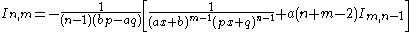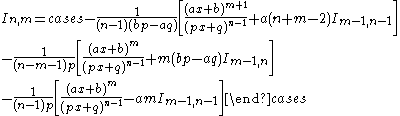| Integral | Reduction formula |
|---|---|
 |
  |
 |
  |
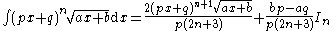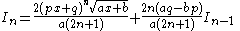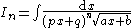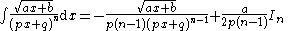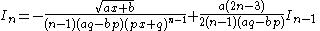| Integral | Reduction formula |
|---|---|
 |
 |
 |
 |
 |
 |
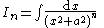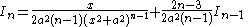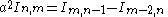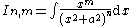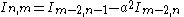| Integral | Reduction formula |
|---|---|
 |
 |
 |
 |
 |
 |
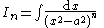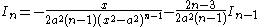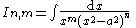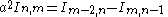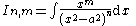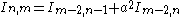| Integral | Reduction formula |
|---|---|
 |
 |
 |
 |
 |
 |
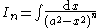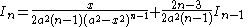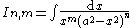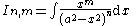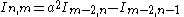| Integral | Reduction formula |
|---|---|
 |
 |
 |
 |
 |
 |
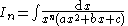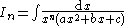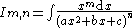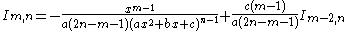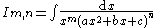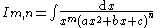| Integral | Reduction formula |
|---|---|
 |
 |
 |
 |
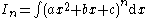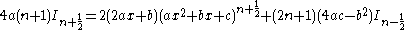note that by the laws of indices
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
:
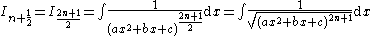
Transcendental functions
See main article: Transcendental functionTranscendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
The following integrals contain:
- Factors of sine
- Factors of cosine
- Factors of sine and cosine products and quotients
- Products/quotients of exponential factors and powers of x
- Products of exponential and sine/cosine factors
| Integral | Reduction formula |
|---|---|
 |
 |
 |
 |
  |
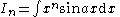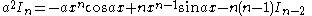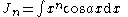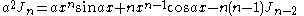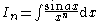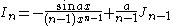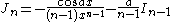  the formulae can be combined to obtain separate equations in In: 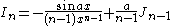 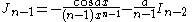 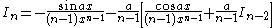 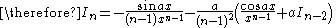 and Jn:     |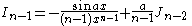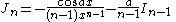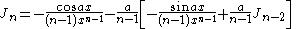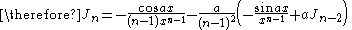
 |
 |
 |
 |
 |
 |
 |
 |
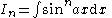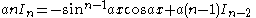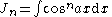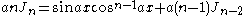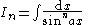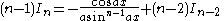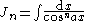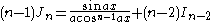| Integral | Reduction formula |
|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
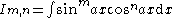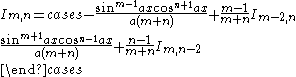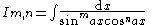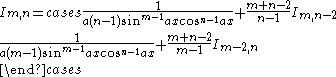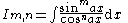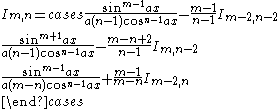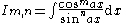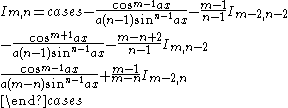| Integral | Reduction formula |
|---|---|
  |
 |
   |
 |
 |
 |
 |
 |
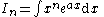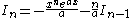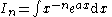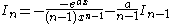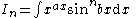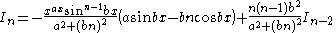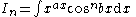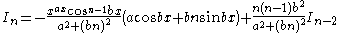Obtaining general integrals
In what follows, all indices are positive integers (natural numbers),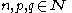.Derivations
Noticing that many of the reduction formulae of one index In (not containing two indices such as Im,n) can be written in the general form: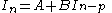where
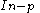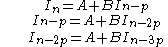
represents a shift of p integrals backwards relative to , and A and B are the collected extra terms (not constants), the general formulae for these integrals can be found by repeated back-substitution:etc., so the general recurrence shift is:
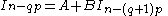
where q is a multiple of p. Performing back substitution to the index n - pq, carefully expanding brackets:
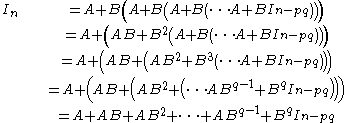
which leads to:
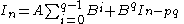
This can be used to obtain the integral as far back as pq indices relative to n, but it helps to transform indices to q, depending on the choice of p (it doesn't matter if n or q is the index). The transform is a simple substitution:
If I0 is known then we can set
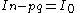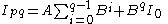
, then so If I1 is known then we can set
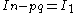, then 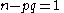so 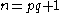Often, as can be seen in the tables above, p = 1 or p = 2, so the reduction formulae can be set up like so:
For  |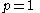
For  |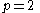
|
 |
 |
 |
 |
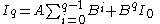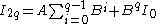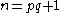 (just an index shift). |
 |
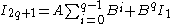These can be used to short-cut the actual repeated use of the reduction formula.
Proof
An inductive proofMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
can show the general formula
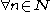to hold . The proof can be split into two in the same way as above;Case 1: one for
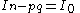so 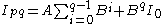Case 2: one for
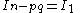so 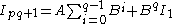For case 2 the index shift is +1, so the proof would be identical to case 1. Only case 1 is proved below.
Case 1:
It can be found that:
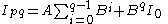
is true for q = 1;
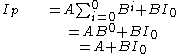
Now assume
is true for some q > 1, then show the formula holds for q + 1:
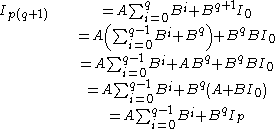
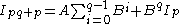
which corresponds to an index shift from I0 to Ip and Ipq to Ipq+p by +p. So the formula must be true
.
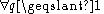