Invariant basis number
Encyclopedia
In mathematics
, the invariant basis number (IBN) property of a ring
R is the property that all free
module
s over R are similarly well-behaved
as vector space
s, with respect to the uniqueness of their ranks.
R has invariant basis number (IBN) if whenever the free left R-module Rm is isomorphic to Rn with m, n finite, then m = n.
(Rn above also has a product ring
structure in addition to that of R-module, but the isomorphism required for IBN is not required to be a ring isomorphism.)
number condition is that free modules over an IBN ring satisfy an analogue of the dimension theorem for vector spaces
: any two bases for a free module over an IBN ring have the same cardinality. Assuming the ultrafilter lemma (a strictly weaker form of the axiom of choice), this result is actually equivalent to the definition given here, and can be taken as an alternative definition.
The rank of a free module Rn over an IBN ring R is defined to be the cardinality of the exponent m of any (and therefore every) R-module Rm isomorphic to Rn. Thus the IBN property asserts that every isomorphism class of free R-modules has a unique rank. The rank is not defined for rings not satisfying IBN. For vector spaces, the rank is also called the dimension. Thus the result above is in short: the rank is uniquely defined for all free R-modules iff
it is uniquely defined for finitely generated free R-modules.
Although in the definition above Rm is viewed as a left R-module, if a ring has invariant basis number with respect to left R-modules, it also has IBN with respect to right R-modules.
(except in the trivial case where 1 = 0) satisfies IBN, as does any left-Noetherian ring and any semilocal ring.
An example of a ring that does not satisfy IBN is the ring of column finite matrices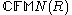
, the matrices with coefficients in a ring R, with entries indexed by 
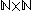and with each column having only finitely many non-zero entries. That last requirement allows to define the product of infinite matrices MN, giving the ring structure. A left module isomorphism 
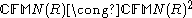is given by: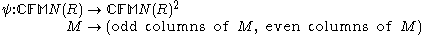
This infinite matrix ring turns out to be isomorphic to the endomorphisms of a right free module
over R of countable rank, which is found on page 190 of .
From this isomorphism, it is possible to show (abbreviating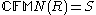
) that S≅Sn for any positive integer n, and hence Sn≅Sm for any two positive integers m and n. There are other examples of non-IBN rings without this property, among them Leavitt algebras as seen in .
(confer field of fractions
in the commutative case). See also the Ore condition
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the invariant basis number (IBN) property of a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R is the property that all free
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s over R are similarly well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
as vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, with respect to the uniqueness of their ranks.
Definition
A ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R has invariant basis number (IBN) if whenever the free left R-module Rm is isomorphic to Rn with m, n finite, then m = n.
(Rn above also has a product ring
Product of rings
In mathematics, it is possible to combine several rings into one large product ring. This is done as follows: if I is some index set and Ri is a ring for every i in I, then the cartesian product Πi in I Ri can be turned into a ring by defining the operations coordinatewise, i.e...
structure in addition to that of R-module, but the isomorphism required for IBN is not required to be a ring isomorphism.)
Discussion
The main purpose of the invariant basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
number condition is that free modules over an IBN ring satisfy an analogue of the dimension theorem for vector spaces
Dimension theorem for vector spaces
In mathematics, the dimension theorem for vector spaces states that all bases of a vector space have equally many elements. This number of elements may be finite, or given by an infinite cardinal number, and defines the dimension of the space....
: any two bases for a free module over an IBN ring have the same cardinality. Assuming the ultrafilter lemma (a strictly weaker form of the axiom of choice), this result is actually equivalent to the definition given here, and can be taken as an alternative definition.
The rank of a free module Rn over an IBN ring R is defined to be the cardinality of the exponent m of any (and therefore every) R-module Rm isomorphic to Rn. Thus the IBN property asserts that every isomorphism class of free R-modules has a unique rank. The rank is not defined for rings not satisfying IBN. For vector spaces, the rank is also called the dimension. Thus the result above is in short: the rank is uniquely defined for all free R-modules iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
it is uniquely defined for finitely generated free R-modules.
Although in the definition above Rm is viewed as a left R-module, if a ring has invariant basis number with respect to left R-modules, it also has IBN with respect to right R-modules.
Examples
Any field satisfies IBN, and this amounts to the fact that finite dimensional vector spaces have a well defined dimension. Moreover, any commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
(except in the trivial case where 1 = 0) satisfies IBN, as does any left-Noetherian ring and any semilocal ring.
An example of a ring that does not satisfy IBN is the ring of column finite matrices
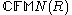, the matrices with coefficients in a ring R, with entries indexed by and with each column having only finitely many non-zero entries. That last requirement allows to define the product of infinite matrices MN, giving the ring structure. A left module isomorphism 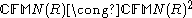is given by: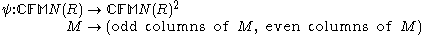This infinite matrix ring turns out to be isomorphic to the endomorphisms of a right free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
over R of countable rank, which is found on page 190 of .
From this isomorphism, it is possible to show (abbreviating
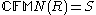) that S≅Sn for any positive integer n, and hence Sn≅Sm for any two positive integers m and n. There are other examples of non-IBN rings without this property, among them Leavitt algebras as seen in .Other results
IBN is a necessary (but not sufficient) condition for a ring with no zero divisors to be embeddable in a division ringDivision ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
(confer field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
in the commutative case). See also the Ore condition
Ore condition
In mathematics, especially in the area of algebra known as ring theory, the Ore condition is a condition introduced by Øystein Ore, in connection with the question of extending beyond commutative rings the construction of a field of fractions, or more generally localization of a ring...
.