
Iso-damping
Encyclopedia
Iso-damping is a desirable system property referring to a state, where the open-loop phase Bode plot
is flat, i.e., the phase derivative with respect to the frequency is zero, at a given frequency called the "tangent frequency" ,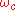 . At the "tangent frequency" the Nyquist curve
. At the "tangent frequency" the Nyquist curve
of the open-loop system tangentially touches the sensitivity circle and the phase Bode is locally flat which implies that the system will be more robust to gain variations. For systems that exhibit iso-damping property, the overshoots
of the closed-loop step response
s will remain almost constant for different values of the controller gain. This will ensure that the closed-loop system is robust to gain variations.
The iso-damping property can be expressed as , or equivalently:
, or equivalently:
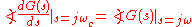 ,
,
where is the tangent frequency and
is the tangent frequency and  is the open-loop system transfer function.
is the open-loop system transfer function.
proposed the first idea involving the use of fractional order control
lers in a feedback problem by what is known as Bode’s Ideal Transfer Function. Bode proposed that the ideal shape of the Nyquist plot
for the open loop frequency response is a straight line in the complex plane, which provides theoretically infinite gain margin. Ideal open-loop transfer function is given by:
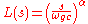
where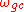 is the desired gain cross over frequency and
is the desired gain cross over frequency and  is the slope of the ideal cut-off characteristic.
is the slope of the ideal cut-off characteristic.
The Bode diagrams of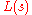 ,
, 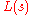 , are very simple. The amplitude curve is a straight line of constant slope
, are very simple. The amplitude curve is a straight line of constant slope  dB/dec, and the phase curve is a horizontal line at
dB/dec, and the phase curve is a horizontal line at  rad. The Nyquist curve
rad. The Nyquist curve
consists of a straight line through the origin with rad.
rad.
The major benefit achieved through this structure is iso-damping, i.e. overshoot being independent of the payload or the system gain. The usage of fractional elements for description of ideal Bode's control loop is one of the most promising applications of fractional calculus
in the process control
field. Bode's ideal control loop frequency response has the fractional integrator shape and provides the iso-damping property around the gain crossover frequency. This is due to the fact that the phase margin
and the maximum overshoot are defined by one parameter only (the fractional power of ), and are independent of open-loop gain.
), and are independent of open-loop gain.
Bode's ideal loop transfer function is probably the first design method that addressed robustness
explicitly.
Bode plot
A Bode plot is a graph of the transfer function of a linear, time-invariant system versus frequency, plotted with a log-frequency axis, to show the system's frequency response...
is flat, i.e., the phase derivative with respect to the frequency is zero, at a given frequency called the "tangent frequency" ,
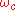 . At the "tangent frequency" the Nyquist curve
. At the "tangent frequency" the Nyquist curveNyquist plot
A Nyquist plot is a parametric plot of a transfer function used in automatic control and signal processing. The most common use of Nyquist plots is for assessing the stability of a system with feedback. In Cartesian coordinates, the real part of the transfer function is plotted on the X axis. The...
of the open-loop system tangentially touches the sensitivity circle and the phase Bode is locally flat which implies that the system will be more robust to gain variations. For systems that exhibit iso-damping property, the overshoots
Overshoot (signal)
In signal processing, control theory, electronics, and mathematics, overshoot is when a signal or function exceeds its target. It arises especially in the step response of bandlimited systems such as low-pass filters...
of the closed-loop step response
Step response
The step response of a system in a given initial state consists of the time evolution of its outputs when its control inputs are Heaviside step functions. In electronic engineering and control theory, step response is the time behaviour of the outputs of a general system when its inputs change from...
s will remain almost constant for different values of the controller gain. This will ensure that the closed-loop system is robust to gain variations.
The iso-damping property can be expressed as
 , or equivalently:
, or equivalently: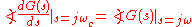 ,
,where
 is the tangent frequency and
is the tangent frequency and  is the open-loop system transfer function.
is the open-loop system transfer function.Bode's Ideal Transfer Function
In the middle of the 20th century, BodeHendrik Wade Bode
Hendrik Wade Bode , was an American engineer, researcher, inventor, author and scientist], of Dutch ancestry. As a pioneer of modern control theory and electronic telecommunications he revolutionized both the content and methodology of his chosen fields of research.He made important contributions...
proposed the first idea involving the use of fractional order control
Fractional order control
Fractional order control or is a field of control theory that uses the fractional order integrator as part of the control system design toolkit....
lers in a feedback problem by what is known as Bode’s Ideal Transfer Function. Bode proposed that the ideal shape of the Nyquist plot
Nyquist plot
A Nyquist plot is a parametric plot of a transfer function used in automatic control and signal processing. The most common use of Nyquist plots is for assessing the stability of a system with feedback. In Cartesian coordinates, the real part of the transfer function is plotted on the X axis. The...
for the open loop frequency response is a straight line in the complex plane, which provides theoretically infinite gain margin. Ideal open-loop transfer function is given by:
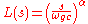
where
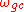 is the desired gain cross over frequency and
is the desired gain cross over frequency and  is the slope of the ideal cut-off characteristic.
is the slope of the ideal cut-off characteristic.The Bode diagrams of
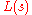 ,
, 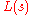 , are very simple. The amplitude curve is a straight line of constant slope
, are very simple. The amplitude curve is a straight line of constant slope  dB/dec, and the phase curve is a horizontal line at
dB/dec, and the phase curve is a horizontal line at  rad. The Nyquist curve
rad. The Nyquist curveNyquist plot
A Nyquist plot is a parametric plot of a transfer function used in automatic control and signal processing. The most common use of Nyquist plots is for assessing the stability of a system with feedback. In Cartesian coordinates, the real part of the transfer function is plotted on the X axis. The...
consists of a straight line through the origin with
 rad.
rad.The major benefit achieved through this structure is iso-damping, i.e. overshoot being independent of the payload or the system gain. The usage of fractional elements for description of ideal Bode's control loop is one of the most promising applications of fractional calculus
Fractional calculus
Fractional calculus is a branch of mathematical analysis that studies the possibility of taking real number powers or complex number powers of the differentiation operator.and the integration operator J...
in the process control
Process control
Process control is a statistics and engineering discipline that deals with architectures, mechanisms and algorithms for maintaining the output of a specific process within a desired range...
field. Bode's ideal control loop frequency response has the fractional integrator shape and provides the iso-damping property around the gain crossover frequency. This is due to the fact that the phase margin
Phase margin
In electronic amplifiers, phase margin is the difference between the phase, measured in degrees, of an amplifier's output signal and 180°, as a function of frequency. The PM is taken as positive at frequencies below where the open-loop phase first crosses 180°, i.e. the signal becomes inverted,...
and the maximum overshoot are defined by one parameter only (the fractional power of
 ), and are independent of open-loop gain.
), and are independent of open-loop gain.Bode's ideal loop transfer function is probably the first design method that addressed robustness
Robust control
Robust control is a branch of control theory that explicitly deals with uncertainty in its approach to controller design. Robust control methods are designed to function properly so long as uncertain parameters or disturbances are within some set...
explicitly.

