
Isogonal conjugate
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the isogonal conjugate of a point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
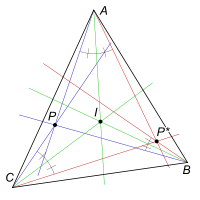
P with respect to a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
ABC is constructed by reflecting
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
the lines PA, PB, and PC about the angle bisectors of A, B, and C. These three reflected lines concur
Concurrent lines
In geometry, two or more lines are said to be concurrent if they intersect at a single point.In a triangle, four basic types of sets of concurrent lines are altitudes, angle bisectors, medians, and perpendicular bisectors:...
at the isogonal conjugate of P. (This definition applies only to points not on a sideline of triangle ABC.)
The isogonal conjugate of a point P is sometimes denoted by P*. The isogonal conjugate of P* is P.
The isogonal conjugate of the incentre I is itself. The isogonal conjugate of the orthocentre H is the circumcentre O. The isogonal conjugate of the centroid
Centroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
G is (by definition) the symmedian point
Symmedian
Symmedians are three particular geometrical lines associated with every triangle. They are constructed by taking a median of the triangle , and reflecting the line over the corresponding angle bisector...
K.
In trilinear coordinates
Trilinear coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
, if X = x : y : z is a point not on a sideline of triangle ABC, then its isogonal conjugate is 1/x : 1/y : 1/z. For this reason, the isogonal conjugate of X is sometimes denoted by X −1. The set S of triangle centers under trilinear product, defined by
- (p : q : r) * (u : v : w) = pu : qv : rw,
is a commutative group, and the inverse of each X in S is X −1.
As isogonal conjugation is a function, it makes sense to speak of the isogonal conjugate of sets of points, such as lines and circles. For example, the isogonal conjugate of a line is a circumconic
Circumconic and inconic
In triangle geometry, a circumconic is a conic section that passes through three given points, and an inconic is a conic section inscribed in the triangle whose vertices lie at three given points....
; specifically, an ellipse, parabola, or hyperbola according as the line intersects the circumcircle in 0, 1, or 2 points. The isogonal conjugate of the circumcircle is the line at infinity. Several well-known cubics (e.g., Thompson cubic, Darboux cubic, Neuberg cubic) are self-isogonal-conjugate, in the sense that if X is on the cubic, then X −1 is also on the cubic.

