Isolation lemma
Encyclopedia
The isolation lemma, also sometimes known as the isolating lemma, is a lemma
in probability theory
with several applications in computer science
. It was introduced in a paper by Mulmuley
, Vazirani
and Vazirani
, who used it to give a randomized parallel algorithm for the maximum matching problem.
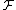be any family of subsets of a set with n elements. Suppose each element x of the set is independently assigned a weight w(x) uniformly from {1, …, N}, and the weight of a set S in 
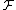is defined as
Then, the probability that there is a unique set in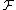
of minimum weight is at least 1−n/N.
The remarkable thing about the lemma is that it assumes nothing about the nature of the family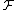
; for instance 
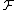may include all 2n subsets, and (as the weight of each set in 
is in {1, …, nN}), there would be an average of 2n/(nN) sets with the same weight. Still, with high probability, there is a unique set of minimum weight.
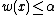, then it is contained in some set of minimum weight. Further, observe that if 
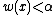, then every minimum-weight subset must contain x (since, when we decrease w(x) from α, sets that do not contain x do not decrease in weight, while those that contain x do). Thus, ambiguity about whether a minimum-weight subset contains x or not can happen only when its weight is exactly equal to its threshold; in this case we will call x "singular". Now, as the threshold of x was defined only in terms of the weights of the other elements, it is independent of w(x), and therefore, as w(x) is chosen uniformly from {1, …, N},
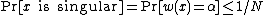
and the probability that some x is singular is at most n/N. As there is a unique minimum-weight subset iff
no element is singular, the lemma follows.
(1995).
For any element x in the set, define
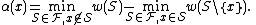
Observe that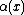
depends only on the weights of elements other than x, and not on w(x) itself. So whatever the value of 
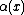, as w(x) is chosen uniformly from {1, …, N}, the probability that it is equal to 
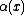is at most 1/N. Thus the probability that 
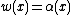for some x is at most n/N.
Now if there are two sets A and B in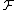
with minimum weight, then, taking any x in A\B, we have
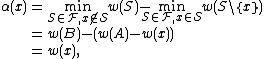
and as we have seen, this event happens with probability at most n/N.
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
with several applications in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
. It was introduced in a paper by Mulmuley
Ketan Mulmuley
Ketan Mulmuley is a professor in the Department of Computer Science at the University of Chicago, and a sometime visiting professor at IIT Bombay...
, Vazirani
Umesh Vazirani
Umesh Virkumar Vazirani is the Roger A. Strauch Professor of Electrical Engineering and Computer Science at the University of California, Berkeley, and the director of the Berkeley Quantum Computation Center. Vazirani was himself a Ph.D. student at Berkeley, receiving his Ph.D. in 1986 under the...
and Vazirani
Vijay Vazirani
Vijay Virkumar Vazirani is an Indian American Professor of Computer Science at Georgia Tech.He received his Bachelor's degree from MIT in 1979 and his Ph.D. from the University of California, Berkeley in 1983. During the early to mid nineties, he was a Professor of Computer Science at the Indian...
, who used it to give a randomized parallel algorithm for the maximum matching problem.
Statement
Let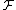 be any family of subsets of a set with n elements. Suppose each element x of the set is independently assigned a weight w(x) uniformly from {1, …, N}, and the weight of a set S in 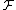is defined asThen, the probability that there is a unique set in
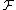of minimum weight is at least 1−n/N.The remarkable thing about the lemma is that it assumes nothing about the nature of the family
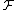; for instance 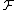may include all 2n subsets, and (as the weight of each set in is in {1, …, nN}), there would be an average of 2n/(nN) sets with the same weight. Still, with high probability, there is a unique set of minimum weight.Proof 1
(The original proof from the paper.) Suppose we have fixed the weights of all elements except an element x. Then x has a threshold weight α, such that if the weight w(x) of x is greater than α, then it is not contained in any minimum-weight subset, and if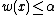, then it is contained in some set of minimum weight. Further, observe that if 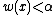, then every minimum-weight subset must contain x (since, when we decrease w(x) from α, sets that do not contain x do not decrease in weight, while those that contain x do). Thus, ambiguity about whether a minimum-weight subset contains x or not can happen only when its weight is exactly equal to its threshold; in this case we will call x "singular". Now, as the threshold of x was defined only in terms of the weights of the other elements, it is independent of w(x), and therefore, as w(x) is chosen uniformly from {1, …, N},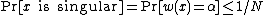and the probability that some x is singular is at most n/N. As there is a unique minimum-weight subset iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
no element is singular, the lemma follows.
Proof 2
This is a restatement version of the above proof, due to Joel SpencerJoel Spencer
Joel Spencer is an American mathematician. He is a combinatorialist who has worked on probabilistic methods in combinatorics and on Ramsey theory. He received his doctorate from Harvard University in 1970, under the supervision of Andrew Gleason...
(1995).
For any element x in the set, define
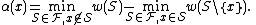
Observe that
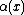depends only on the weights of elements other than x, and not on w(x) itself. So whatever the value of 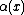, as w(x) is chosen uniformly from {1, …, N}, the probability that it is equal to 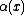is at most 1/N. Thus the probability that 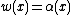for some x is at most n/N.Now if there are two sets A and B in
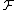with minimum weight, then, taking any x in A\B, we have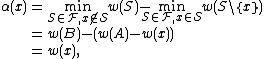and as we have seen, this event happens with probability at most n/N.
Examples/applications
- The original application was to minimum-weight (or maximum-weight) perfect matchings in a graph. Each edge is assigned a random weight in {1, …, 2m}, and
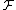is the set of perfect matchings, so that with probability at least 1/2, there exists a unique perfect matching. When each indeterminate 
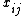in the Tutte matrixTutte matrixIn graph theory, the Tutte matrix A of a graph G = is a matrix used to determine the existence of a perfect matching: that is, a set of edges which is incident with each vertex exactly once....
of the graph is replaced with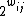
where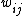 
is the random weight of the edge, we can show that the determinant of the matrix is nonzero, and further use this to find the matching.
- More generally, the paper also observed that any search problem of the form "Given a set system
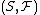, find a set in 
" could be reduced to a decision problem of the form "Is there a set in 
with total weight at most k?". For instance, it showed how to solve the following problem posed by Papadimitriou and Yannakakis, for which (as of the time the paper was written) no deterministic polynomial-time algorithm is known: given a graph and a subset of the edges marked as "red", find a perfect matching with exactly k red edges.
- The Valiant–Vazirani theorem, concerning unique solutions to NP-complete problems, has a simpler proof using the isolation lemma. This is proved by giving a randomized reduction from CLIQUEClique problemIn computer science, the clique problem refers to any of the problems related to finding particular complete subgraphs in a graph, i.e., sets of elements where each pair of elements is connected....
to UNIQUE-CLIQUE.
- Avi WigdersonAvi WigdersonAvi Wigderson is an Israeli mathematician and computer scientist, a professor of mathematics at the Institute for Advanced Study in Princeton. His research interests include complexity theory, parallel algorithms, graph theory, cryptography, distributed computing, and neural...
used the isolation lemma in 1994 to give a randomized reduction from NLNL (complexity)In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space....
to UL, and thereby prove that NL/poly ⊆ ⊕L/poly. Reinhardt and Allender later used the isolation lemma again to prove that NL/poly = UL/poly.
- The book by Hemaspaandra and Ogihara has a chapter on the isolation technique, including generalizations.
- The isolation lemma has been proposed as the basis of a scheme for digital watermarkingDigital watermarkingDigital watermarking is the process of embedding information into a digital signal which may be used to verify its authenticity or the identity of its owners, in the same manner as paper bearing a watermark for visible identification. In digital watermarking, the signal may be audio, pictures, or...
.
- There is ongoing work on derandomizing the isolation lemma in specific cases and on using it for identity testing.
External links
- Favorite Theorems: Unique Witnesses by Lance FortnowLance FortnowLance Jeremy Fortnow is a computer scientist in the field of computational complexity and its applications, notable for producing major results on interactive proof systems.-Biography:...
- The Isolation Lemma and Beyond by Richard J. LiptonRichard J. LiptonRichard Jay "Dick" Lipton is an American computer scientist who has worked in computer science theory, cryptography, and DNA computing. Lipton is presently Associate Dean of Research, Professor, and the Frederick G...