Richard J. Lipton
Encyclopedia
Richard Jay "Dick" Lipton is an American
computer scientist
who has worked in computer science theory, cryptography
, and DNA computing
. Lipton is presently Associate Dean of Research, Professor, and the Frederick G. Storey Chair in Computing in the College of Computing at the Georgia Institute of Technology
.
from Case Western Reserve University
. In 1973, he received his Ph.D.
from Carnegie Mellon University
; his dissertation, supervised by David Parnas
, is entitled On Synchronization Primitive Systems. After graduating, Lipton taught at Yale
1973–1978, at Berkeley
1978–1980, and then at Princeton
1980–2000. Since 2000, Lipton has been at Georgia Tech
. While at Princeton, Lipton worked in the field of DNA computing
. Since 1996, Lipton has been the chief consulting scientist at Telcordia.
can be solved by Boolean circuit
s with a polynomial number of logic gate
s, then the polynomial hierarchy
collapses to its second level.
, the 2-size version being strongly competitive, and the k-size version achieving O(log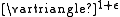
), as well as demonstrating a theoretical lower-bound of O(log
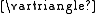). This algorithm uses a private-coin for randomization and a "virtual" choice to fool a medium adversary
.
Being presented with an event the user must decide whether or not to include the event in the schedule. The 2-size virtual algorithm is described by how it reacts to 1-interval or k-intervals being presented by the adversary:
Again, this 2-size algorithm is shown to be strongly-competitive
. The generalized k-size algorithm which is similar to the 2-size algorithm is then shown to be O(log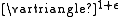
)-competitive.
This technique is useful to check the correctness of many types of problems.
, more specifically on non-cooperative game
, Lipton together with E.Markakis and A.Mehta proved the existence of epsilon-equilibrium
strategies with support logarithmic in the number of pure strategy. Furthermore, the payoff of such strategies can epsilon-approximate the payoffs of exact Nash equilibrium
. The limited size (logarithmic) of support provides a natural quasi-polynomial algorithm of computing an epsilon-equilibrium
.
, 
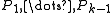) have access to a set of integers (
, 
,…
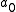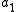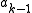) except one of them, so that 
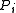is denied access to 
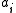. These processes are allowed to communicate in order to arrive at a consensus on a predicate. They studied this model’s communication complexity, defined as the number of bits broadcast among all the processes. As an example, they studied the complexity of a k-party protocol for Exactly-N (do all 
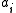’s sum up to N?), and obtained a lower bound using the tiling method. They further applied this model to study general branching programs and obtained a time lower bound for constant-space branching programs that compute Exactly-N.
(often abbreviated as SAT), which is NP-complete
, requires exponential (or at least super-polynomial) time (this is the famous P versus NP problem), or linear (or at least super-logarithmic) space to solve. However, in the context of space-time tradeoff
, one can prove that SAT cannot be computed if we apply constraints to both time and space. L. Fortnow, Lipton, D. van Melkebeek, and A. Viglas proved that SAT cannot be computed by a Turing machine that takes at most O(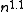
) steps and at most O(
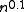) cells of its read-write tapes.
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
computer scientist
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
who has worked in computer science theory, cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, and DNA computing
DNA computing
DNA computing is a form of computing which uses DNA, biochemistry and molecular biology, instead of the traditional silicon-based computer technologies. DNA computing, or, more generally, biomolecular computing, is a fast developing interdisciplinary area...
. Lipton is presently Associate Dean of Research, Professor, and the Frederick G. Storey Chair in Computing in the College of Computing at the Georgia Institute of Technology
Georgia Institute of Technology
The Georgia Institute of Technology is a public research university in Atlanta, Georgia, in the United States...
.
Career
In 1968, Lipton received his undergraduate degree in mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
from Case Western Reserve University
Case Western Reserve University
Case Western Reserve University is a private research university located in Cleveland, Ohio, USA...
. In 1973, he received his Ph.D.
Ph.D.
A Ph.D. is a Doctor of Philosophy, an academic degree.Ph.D. may also refer to:* Ph.D. , a 1980s British group*Piled Higher and Deeper, a web comic strip*PhD: Phantasy Degree, a Korean comic series* PhD Docbook renderer, an XML renderer...
from Carnegie Mellon University
Carnegie Mellon University
Carnegie Mellon University is a private research university in Pittsburgh, Pennsylvania, United States....
; his dissertation, supervised by David Parnas
David Parnas
David Lorge Parnas is a Canadian early pioneer of software engineering, who developed the concept of information hiding in modular programming, which is an important element of object-oriented programming today. He is also noted for his advocacy of precise documentation.- Biography :Parnas earned...
, is entitled On Synchronization Primitive Systems. After graduating, Lipton taught at Yale
Yale University
Yale University is a private, Ivy League university located in New Haven, Connecticut, United States. Founded in 1701 in the Colony of Connecticut, the university is the third-oldest institution of higher education in the United States...
1973–1978, at Berkeley
University of California, Berkeley
The University of California, Berkeley , is a teaching and research university established in 1868 and located in Berkeley, California, USA...
1978–1980, and then at Princeton
Princeton University
Princeton University is a private research university located in Princeton, New Jersey, United States. The school is one of the eight universities of the Ivy League, and is one of the nine Colonial Colleges founded before the American Revolution....
1980–2000. Since 2000, Lipton has been at Georgia Tech
Georgia Institute of Technology
The Georgia Institute of Technology is a public research university in Atlanta, Georgia, in the United States...
. While at Princeton, Lipton worked in the field of DNA computing
DNA computing
DNA computing is a form of computing which uses DNA, biochemistry and molecular biology, instead of the traditional silicon-based computer technologies. DNA computing, or, more generally, biomolecular computing, is a fast developing interdisciplinary area...
. Since 1996, Lipton has been the chief consulting scientist at Telcordia.
Karp–Lipton theorem
In 1980, along with Richard M. Karp, Lipton proved that if SATBoolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
can be solved by Boolean circuit
Boolean circuit
A Boolean circuit is a mathematical model of computation used in studying computational complexity theory. Boolean circuits are the main object of study in circuit complexity and are a special kind of circuits; a formal language can be decided by a family of Boolean circuits, one circuit for each...
s with a polynomial number of logic gate
Logic gate
A logic gate is an idealized or physical device implementing a Boolean function, that is, it performs a logical operation on one or more logic inputs and produces a single logic output. Depending on the context, the term may refer to an ideal logic gate, one that has for instance zero rise time and...
s, then the polynomial hierarchy
Polynomial hierarchy
In computational complexity theory, the polynomial hierarchy is a hierarchy of complexity classes that generalize the classes P, NP and co-NP to oracle machines...
collapses to its second level.
Parallel algorithms
Showing that a program P has some property is a simple process if the actions inside the program are uninterruptible. However, when the action is interruptible, Lipton showed that through a type of reduction and analysis, it can be shown that the reduced program has that property if and only if the original program has the property. If the reduction is done by treating interruptible operations as one large uninterruptible action, even with these relaxed conditions properties can be proven for a program P. Thus, correctness proofs of a parallel system can often be greatly simplified.Database security
Lipton studied and created database security models on how and when to restrict the queries made by users of a database such that private or secret information will not be leaked. Even when the user is restricted to only read operations on a database, secure information could be at risk. For example, querying a database of campaign donations could allow the user to discover the individual donations to political candidates or organizations. If given access to averages of data and unrestricted query access, a user could exploit the properties of those averages to gain illicit information. These queries are considered to have large "overlap" creating the insecurity. By bounding the "overlap" and number of queries, a secure database can be achieved.Online scheduling
Richard Lipton with Andrew Tomkins introduced a randomized online interval scheduling algorithmAdversary (online algorithm)
In computer science, an online algorithm measures its competitiveness against different adversary models. For deterministic algorithms, the adversary is the same, the adaptive offline adversary...
, the 2-size version being strongly competitive, and the k-size version achieving O(log
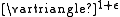), as well as demonstrating a theoretical lower-bound of O(log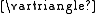). This algorithm uses a private-coin for randomization and a "virtual" choice to fool a medium adversaryAdversary (online algorithm)
In computer science, an online algorithm measures its competitiveness against different adversary models. For deterministic algorithms, the adversary is the same, the adaptive offline adversary...
.
Being presented with an event the user must decide whether or not to include the event in the schedule. The 2-size virtual algorithm is described by how it reacts to 1-interval or k-intervals being presented by the adversary:
- For a 1-interval, flip a fair coin
-
- Heads: Take the interval
- Tails: "Virtually" take the interval, but do no work. Take no short interval for the next 1 unit of time.
-
- For a k-interval, take whenever possible.
Again, this 2-size algorithm is shown to be strongly-competitive
Competitive analysis (online algorithm)
Competitive analysis is a method invented for analyzing online algorithms, in which the performance of an online algorithm is compared to the performance of an optimal offline algorithm that can view the sequence of requests in advance...
. The generalized k-size algorithm which is similar to the 2-size algorithm is then shown to be O(log
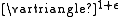)-competitive.Program checking
Lipton showed that randomized testing can be provably useful, given the problem satisfied certain properties. Proving correctness of a program is one of the most important problems presented in computer science. Typically in randomized testing, in order to attain a 1/1000 chance of an error, 1000 tests must be run. However Lipton shows that if a problem has "easy" sub-parts, repeated black-box testing can attain cr error rate, with c a constant less than 1 and r being the number of tests. Therefore, the probability of error goes to zero exponentially fast as r grows.This technique is useful to check the correctness of many types of problems.
- Signal processing: fast Fourier transform (FFT)Fast Fourier transformA fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
and other highly parallelizable functions are difficult to manually check results when written in code such as FORTRANFortranFortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
, so a way to quickly check correctness is greatly desired. - Functions over finite fields and the permanent: Suppose that
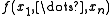is a polynomial over a finite field of size q with q > deg(ƒ) + 1. Then ƒ is randomly testable of order deg(ƒ) + 1 over the function basis that includes just addition. Perhaps the most important application from this is the ability to efficiently check the correctness of the permanentPermanentThe permanent of a square matrix in linear algebra, is a function of the matrix similar to the determinant. The permanent, as well as the determinant, is a polynomial in the entries of the matrix...
. Cosmetically similar to the determinant, the permanent is very difficult to check correctness, but even this type of problem satisfies the constraints. This result even led to the breakthroughs of interactive proof systemInteractive proof systemIn computational complexity theory, an interactive proof system is an abstract machine that models computation as the exchange of messages between two parties. The parties, the verifier and the prover, interact by exchanging messages in order to ascertain whether a given string belongs to a...
s Karloff-Nisan and Shamir, including the result IP = PSPACE.
Games with simple strategies
In the area of game theoryGame theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, more specifically on non-cooperative game
Non-cooperative game
In game theory, a non-cooperative game is one in which players make decisions independently. Thus, while they may be able to cooperate, any cooperation must be self-enforcing....
, Lipton together with E.Markakis and A.Mehta proved the existence of epsilon-equilibrium
Epsilon-equilibrium
In game theory, an epsilon-equilibrium, or near-Nash equilibrium, is a strategy profile that approximately satisfies the condition of Nash equilibrium.- Definition :Given a game and a real non-negative parameter ε, a strategy profile is said to be an...
strategies with support logarithmic in the number of pure strategy. Furthermore, the payoff of such strategies can epsilon-approximate the payoffs of exact Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
. The limited size (logarithmic) of support provides a natural quasi-polynomial algorithm of computing an epsilon-equilibrium
Epsilon-equilibrium
In game theory, an epsilon-equilibrium, or near-Nash equilibrium, is a strategy profile that approximately satisfies the condition of Nash equilibrium.- Definition :Given a game and a real non-negative parameter ε, a strategy profile is said to be an...
.
Query size estimation
Lipton and J.Naughton presented an adaptive random sampling algorithm for database querying which is applicable to any query for which answer to the query can be partitioned into disjoint subsets. Compared with most sampling estimation algorithms that statically determines the number of samples needed, the algorithm they proposed decides the number of samples based on the size of samples and tends to keep the running time constant rather than the number of samples.Formal verification of programs
De Millo, Lipton and Perlis criticized the idea of formal verification of programs and argued that- Formal verifications in computer science will not play the same key role as proofs do in mathematics.
- Absence of continuity, the inevitability of change, and the complexity of specification of real programs will make formal verification of programs difficult to justify and manage.
Multi-party protocols
Chandra, Furst and Lipton generalized the notion of two-party communication protocols to multi-party communication protocols. They proposed a model in which a collection of processes (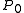, 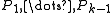) have access to a set of integers (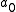, ,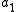… 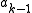) except one of them, so that 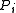is denied access to 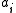. These processes are allowed to communicate in order to arrive at a consensus on a predicate. They studied this model’s communication complexity, defined as the number of bits broadcast among all the processes. As an example, they studied the complexity of a k-party protocol for Exactly-N (do all 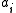’s sum up to N?), and obtained a lower bound using the tiling method. They further applied this model to study general branching programs and obtained a time lower bound for constant-space branching programs that compute Exactly-N.Time/space SAT tradeoff
Currently we have no way to prove that Boolean satisfiability problemBoolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
(often abbreviated as SAT), which is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
, requires exponential (or at least super-polynomial) time (this is the famous P versus NP problem), or linear (or at least super-logarithmic) space to solve. However, in the context of space-time tradeoff
Space-time tradeoff
In computer science, a space–time or time–memory tradeoff is a situation where the memory use can be reduced at the cost of slower program execution...
, one can prove that SAT cannot be computed if we apply constraints to both time and space. L. Fortnow, Lipton, D. van Melkebeek, and A. Viglas proved that SAT cannot be computed by a Turing machine that takes at most O(
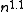) steps and at most O(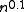) cells of its read-write tapes.Awards and honors
- Guggenheim FellowGuggenheim FellowshipGuggenheim Fellowships are American grants that have been awarded annually since 1925 by the John Simon Guggenheim Memorial Foundation to those "who have demonstrated exceptional capacity for productive scholarship or exceptional creative ability in the arts." Each year, the foundation makes...
, 1981 - FellowFellowA fellow in the broadest sense is someone who is an equal or a comrade. The term fellow is also used to describe a person, particularly by those in the upper social classes. It is most often used in an academic context: a fellow is often part of an elite group of learned people who are awarded...
of the Association for Computing MachineryAssociation for Computing MachineryThe Association for Computing Machinery is a learned society for computing. It was founded in 1947 as the world's first scientific and educational computing society. Its membership is more than 92,000 as of 2009...
, 1997 - member of the National Academy of EngineeringNational Academy of EngineeringThe National Academy of Engineering is a government-created non-profit institution in the United States, that was founded in 1964 under the same congressional act that led to the founding of the National Academy of Sciences...