Isotopy of quasigroups

Let and 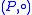be quasigroups. A quasigroup homotopy from Q to P is a triple (α, β, γ) of maps from Q to P such that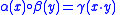
for all x, y in Q. A quasigroup homomorphism is just a homotopy for which the three maps are equal.

An isotopy is a homotopy for which each of the three maps (α, β, γ) is a bijection

Bijection

A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...

. Two quasigroups are isotopic if there is an isotopy between them. In terms of Latin squares, an isotopy (α, β, γ) is given by a permutation of rows α, a permutation of columns β, and a permutation on the underlying element set γ.

An autotopy is an isotopy from a quasigroup 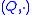to itself. The set of all autotopies of a quasigroup form a group with the automorphism group as a subgroup.

A principal isotopy is an isotopy for which γ is the identity map on Q. In this case the underlying sets of the quasigroups must be the same but the multiplications may differ.

Each quasigroup is isotopic to a loop.

Isotopy of loops

Let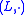 and be loops and let 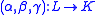be an isotopy. Then it is the product of the principal isotopy 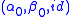from 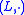and 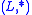and the isomorphism between and 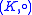. Indeed, put 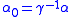, and define the operation * by .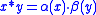

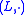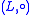Let and be loops and let e be the neutral element of 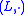. Let 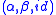a principal isotopy from 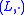to 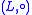. Then 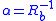and 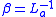where and .

A loop L is a G-loop if it is isomorphic to all its loop isotopes.

Pseudo-automorphisms of loops

Let L be a loop and c an element of L. A bijection α of L is called a right pseudo-automorphism of L with companion element c if for all x, y the identity
holds. One defines left pseudo-automorphisms analogously.

Universal properties

We say that a loop property P is universal if it is isotopy invariant, that is, P holds for a loop L if and only if P holds for all isotopes of L. Clearly, it is enough to check if P holds for all principal isotopes of L.

For example, since the isotopes of a commutative loop need not be commutative, commutativity

Commutativity

In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...

 is not universal. However, associativity

Associativity

In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...

 and being an abelian group

Abelian group

In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...

 are universal properties. In fact, every group is a G-loop.

The geometric interpretation of isotopy

Given a loop L, one can define an incidence geometric structure called a 3-net. Conversely, after fixing an origin and an order of the line classes, a 3-net gives rise to a loop. Choosing a different origin or exchanging the line classes may result in nonisomorphic coordinate loops. However, the coordinate loops are always isotopic. In other words, two loops are isotopic if and only if they are equivalent from geometric point of view.

The dictionary between algebraic and geometric concepts is as follows

• The group of autotopism of the loop corresponds to the group direction preserving collineations of the 3-net.
• Pseudo-automorphisms correspond to collineations fixing the two axis of the coordinate system.
• The set of companion elements is the orbit of the stabilizer of the axis in the collineation group.
• The loop is G-loop if and only if the collineation group acts transitively on the set of point of the 3-net.
• The property P is universal if and only if it is independent on the choice of the origin.