
Isotropic line
Encyclopedia
An isotropic line or null line is a line in the complex projective plane with slope  or
or 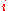
 or
or 
or, in matrix
-notation, or
or 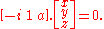
 or
or 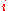
Equation
All isotropic lines have equations of the following form: or
or 
or, in matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
-notation,
 or
or 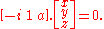
Properties
- An isotropic line is perpendicularPerpendicularIn geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to itself - The euclidean distanceEuclidean distanceIn mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
between two points on an isotropic line is zero (hence null line) - The unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of two conjugate isotropic lines is a circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius.... - The point at infinity of an isotropic line is always one of the two circular points at infinityCircular points at infinityIn projective geometry, the circular points at infinity in the complex projective plane are and ....
- If an isotropic line is rotated 90 degrees its image is itself

