
Iterated monodromy group
Encyclopedia
In geometric group theory
and dynamical systems the iterated monodromy group of a covering map
is a group
describing the monodromy action of the fundamental group
on all iteration
s of the covering. It encodes the combinatorics and symbolic dynamics
of the covering and is an example of a self-similar group.
:
where :
of preimages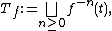
where a vertex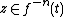 is connected by an edge with
is connected by an edge with 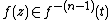 .
.
If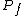 is finite (or has a finite set of accumulation points), then the iterated monodromy group of f is the iterated monodromy group of the covering
is finite (or has a finite set of accumulation points), then the iterated monodromy group of f is the iterated monodromy group of the covering 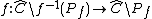 , where
, where 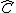 is the Riemann sphere
is the Riemann sphere
.
Iterated monodromy groups of rational functions usually have exotic properties from the point of view of classical group theory. Most of them are infinitely presented, many have intermediate growth.
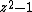
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
and dynamical systems the iterated monodromy group of a covering map
Covering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
describing the monodromy action of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
on all iteration
Iteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
s of the covering. It encodes the combinatorics and symbolic dynamics
Symbolic dynamics
In mathematics, symbolic dynamics is the practice of modeling a topological or smooth dynamical system by a discrete space consisting of infinite sequences of abstract symbols, each of which corresponds to a state of the system, with the dynamics given by the shift operator...
of the covering and is an example of a self-similar group.
Definition
The Iterated monodromy group of f is the following quotient groupQuotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
:

where :
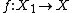 be a coveringCovering mapIn mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
be a coveringCovering mapIn mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
of a path-connected and locally path-connected topological space X by its subset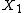 ,
,-
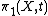 be the fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
be the fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of X and
-
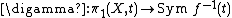 be the monodromy action for f.
be the monodromy action for f.
-
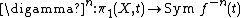 be the monodromy action of the
be the monodromy action of the 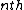 iteration of f,
iteration of f,  .
.
Action
The iterated monodromy group acts by automorphism on the rooted treeTree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
of preimages
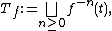
where a vertex
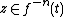 is connected by an edge with
is connected by an edge with 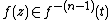 .
.Iterator monodromy groups of rational functions
Let :- f be a complex rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
-
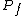 be the union of forward orbitsOrbit (dynamics)In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
be the union of forward orbitsOrbit (dynamics)In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
of its critical pointsCritical point (mathematics)In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
(the post-critical set).
If
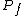 is finite (or has a finite set of accumulation points), then the iterated monodromy group of f is the iterated monodromy group of the covering
is finite (or has a finite set of accumulation points), then the iterated monodromy group of f is the iterated monodromy group of the covering 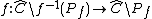 , where
, where 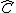 is the Riemann sphere
is the Riemann sphereRiemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
.
Iterated monodromy groups of rational functions usually have exotic properties from the point of view of classical group theory. Most of them are infinitely presented, many have intermediate growth.
IMG of polynomials
Basilica group is the iterated monodromy group of the polynomial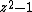
See also
- Growth rate (group theory)Growth rate (group theory)In group theory, the growth rate of a group with respect to a symmetric generating set describes the size of balls in the group. Every element in the group can be written as a product of generators, and the growth rate counts the number of elements that can be written as a product of length...
- amenable groupAmenable groupIn mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...
- complex dynamicsComplex dynamicsComplex dynamics is the study of dynamical systems defined by iteration of functions on complex number spaces. Complex analytic dynamics is the study of the dynamics of specifically analytic functions.-Techniques:*General** Montel's theorem...
- Julia setJulia setIn the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
External links
- arXiv.org - Iterated Monodromy Group - preprints about the Iterated Monodromy Group.
- Laurent Bartholdi's page - Movies illustrating the Dehn twists about a Julia setJulia setIn the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
. - mathworld.wolfram.com - The Monodromy Group page.

