Jack function
Encyclopedia
In mathematics
, the Jack function, introduced by Henry Jack
, is a homogenous
, symmetric
polynomial
which generalizes the Schur
and zonal
polynomials,
and is in turn generalized by the Heckman–Opdam polynomials
and Macdonald polynomial
s.
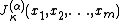
of integer partition
, parameter 
and
arguments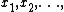
can be recursively defined as
follows:
For m=1 :
For m>1:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Jack function, introduced by Henry Jack
Henry Jack
Henry Jack was a Scottish mathematician at University College Dundee. The Jack polynomials are named after him. His research dealt with the development of analytic methods to evaluate certain integrals over matrix spaces. His most famous paper relates his integrals to classes of symmetric...
, is a homogenous
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
, symmetric
Symmetric polynomial
In mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
which generalizes the Schur
Schur polynomial
In mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of...
and zonal
Zonal polynomial
In mathematics, a zonal polynomial is a multivariate symmetric homogeneous polynomial. The zonal polynomials form a basis of the space of symmetric polynomials.They appear as zonal spherical functions of the Gelfand pairs...
polynomials,
and is in turn generalized by the Heckman–Opdam polynomials
Heckman–Opdam polynomials
In mathematics, Heckman–Opdam polynomials Pλ are orthogonal polynomials in several variables associated to root systems...
and Macdonald polynomial
Macdonald polynomial
In mathematics, Macdonald polynomials Pλ are a family of orthogonal polynomials in several variables, introduced by...
s.
Definition
The Jack function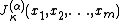of integer partition
, parameter andarguments
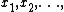can be recursively defined asfollows:
For m=1 :
For m>1:
-
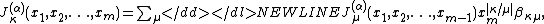
where the summation is over all partitions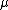
such that the skew partition 
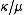is a horizontal strip, namely
(
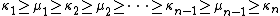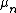must be zero or otherwise 
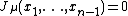) and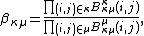
where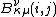
equals 
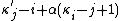if 
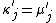and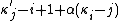 
otherwise. The expressions 
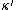and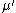 
refer to the conjugate partitions of 
and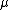 
, respectively. The notation 
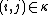means that the product is taken over all coordinates 
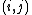of boxes in the Young diagram of the partition 
.
C normalization
The Jack functions form an orthogonal basis in a space of symmetric polynomials. This orthogonality property is unaffected by normalization. The normalization defined above is typically referred to as the J normalization. The C normalization is defined as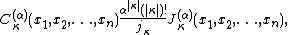
where
For
denoted often as just
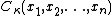is known as the Zonal polynomialZonal polynomialIn mathematics, a zonal polynomial is a multivariate symmetric homogeneous polynomial. The zonal polynomials form a basis of the space of symmetric polynomials.They appear as zonal spherical functions of the Gelfand pairs...
.
Connection with the Schur polynomial
When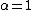
the Jack function is a scalar multiple of the Schur polynomialSchur polynomialIn mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of...
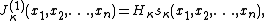
where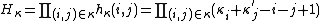
is the product of all hook lengths of
.
Properties
If the partition has more parts than the number of variables, then the Jack function is 0:
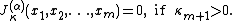
Matrix argument
In some texts, especially in random matrix theory, authors have found it more convenient to use a matrix argument in the Jack function. The connection is simple. If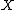
is a matrix with eigenvalues
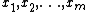, then
External links