Macdonald polynomial
Encyclopedia
In mathematics, Macdonald polynomials Pλ(x; t,q) are a family of orthogonal polynomials
in several variables, introduced by . Macdonald originally associated his polynomials with weights λ of finite root systems and used just one variable t, but later realized that it is more natural to associate them with affine root system
s rather than finite root systems, in which case the variable t can be replaced by several different variables t=(t1,...,tk), one for each of the k orbits of roots in the affine root system. The Macdonald polynomials are polynomials in n variables x=(x1,...,xn), where n is the rank of the affine root system. They generalize many other families of orthogonal polynomials, such as Jack polynomials and Hall–Littlewood polynomial
s and Askey–Wilson polynomials
, which in turn include most of the named 1-variable orthogonal polynomials as special cases. Koornwinder polynomials
are Macdonald polynomials of certain non-reduced root systems. They have deep relationships with affine Hecke algebra
s and Hilbert scheme
s, which were used to prove several conjectures made by Macdonald about them.
The Macdonald polynomials Pλ for λ ∈ P+ are uniquely defined by the following two conditions: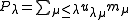
where uλμ is a rational function of q and t with uλλ = 1;
In other words the Macdonald polynomials are obtained by orthogonalizing the obvious basis for AW. The existence of polynomials with these properties is easy to show (for any inner product). A key property of the Macdonald polynomials is that they are orthogonal: 〈Pλ, Pμ〉 = 0 whenever λ ≠ μ. This is not a trivial consequence of the definition because P+ is not totally ordered, so has plenty of elements that are incomparable, and one has to check that the corresponding polynomials are still orthogonal. The orthogonality can be proved by showing that the Macdonald polynomials are eigenvectors
for an algebra of commuting self adjoint operators with 1-dimensional eigenspaces, and using the fact that eigenspaces for different eigenvalues must be orthogonal.
In the case of non-simply-laced root systems (B, C, F, G), the parameter t can be chosen to vary with the length of the root, giving a three-parameter family of Macdonald polynomials. One can also extend the definition to the nonreduced root system BC, in which case one obtains a six-parameter family (one t for each orbit of roots, plus q) known as Koornwinder polynomials
. It is sometimes better to regard Macdonald polynomials as depending on a possibly non-reduced affine root system. In this case there is one parameter t associated to each orbit of roots in the affine root system, plus one parameter q. The number of orbits of roots can vary from 1 to 5.
Koornwinder polynomials
.
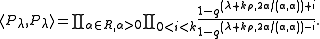
This was conjectured by Macdonald (1982) as a generalization of the Dyson conjecture
, and proved for all (reduced) root systems by Cherednik (1995) using properties of double affine Hecke algebra
s. The conjecture had previously been proved case-by-case for all roots systems except those of type En by several authors.
There are two other conjectures which together with the norm conjecture are collectively referred to as the Macdonald conjectures in this context: in addition to the formula for the norm, Macdonald conjectured a formula for the value of Pλ at the point tρ, and a symmetry
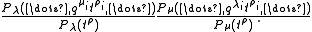
Again, these were proved for general reduced root systems by , using double affine Hecke algebra
s, with the extension to the BC case following shortly thereafter via work of van Diejen, Noumi, and Sahi.
can be identified with symmetric polynomials in n variables (with coefficients that are rational functions of q and t). They can be expanded in terms of Schur functions, and the coefficients Kλμ(q,t) of these expansions are called Kostka–Macdonald coefficients.
Macdonald conjectured that the Kostka–Macdonald coefficients were polynomials in q and t with non-negative integer coefficients. These conjectures are now proved; the hardest and final step was proving the positivity, which was done by Mark Haiman
(2001), by proving the n! conjecture.
and Mark Haiman
states that for each partition μ of n the space
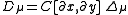
spanned by all higher partial derivatives of
has dimension n!, where (pj, qj) run through the n elements of the diagram of the partition μ, regarded as a subset of the pairs of non-negative integers.
For example, if μ is the partition 3 = 2 + 1 of n = 3 then the pairs (pj, qj) are
(0, 0), (0, 1), (1, 0), and the space Dμ is spanned by
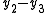
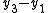
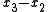
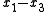
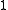
which has dimension 6 = 3! .
Haiman's proof of the Macdonald positivity conjecture and the n! conjecture involved showing that the isospectral Hilbert scheme of n points in a plane was Cohen–Macaulay (and even Gorenstein
). Earlier results of Haiman and Garsia had already shown that this implied the n! conjecture, and that the n! conjecture implied that the Kostka–Macdonald coefficients were graded character multiplicities for the modules Dμ. This immediately implies the Macdonald positivity conjecture because character multiplicities have to be non-negative integers.
Ian Grojnowski and Mark Haiman found another proof of the Macdonald positivity conjecture by proving a positivity conjecture for LLT polynomial
s.
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
in several variables, introduced by . Macdonald originally associated his polynomials with weights λ of finite root systems and used just one variable t, but later realized that it is more natural to associate them with affine root system
Affine root system
In mathematics, an affine root system is a root system of affine-linear functions on a Euclidean space. They are used in the classification of affine Lie algebras and superalgebras, and semisimple p-adic algebraic groups, and correspond to families of Macdonald polynomials. The reduced affine root...
s rather than finite root systems, in which case the variable t can be replaced by several different variables t=(t1,...,tk), one for each of the k orbits of roots in the affine root system. The Macdonald polynomials are polynomials in n variables x=(x1,...,xn), where n is the rank of the affine root system. They generalize many other families of orthogonal polynomials, such as Jack polynomials and Hall–Littlewood polynomial
Hall–Littlewood polynomial
In mathematics, the Hall–Littlewood polynomials are symmetric functions depending on a parameter t and a partition λ. They are Schur functions when t is 0 and monomial symmetric functions when t is 1 and are special cases of Macdonald polynomials.They were first defined indirectly by ...
s and Askey–Wilson polynomials
Askey–Wilson polynomials
In mathematics, the Askey–Wilson polynomials are a family of orthogonal polynomials introduced by as q-analogs of the Wilson polynomials. They include many of the other orthogonal polynomials in 1 variable as special or limiting cases, described in the Askey scheme...
, which in turn include most of the named 1-variable orthogonal polynomials as special cases. Koornwinder polynomials
Koornwinder polynomials
In mathematics, Koornwinder polynomials are a family of orthogonal polynomials in several variables, introduced by , that generalize the Askey-Wilson polynomials...
are Macdonald polynomials of certain non-reduced root systems. They have deep relationships with affine Hecke algebra
Affine Hecke algebra
In mathematics, an affine Hecke algebra is the Hecke algebra of an affine Weyl group, and can be used to prove Macdonald's constant term conjecture for Macdonald polynomials.-Definition:...
s and Hilbert scheme
Hilbert scheme
In algebraic geometry, a branch of mathematics, a Hilbert scheme is a scheme that is the parameter space for the closed subschemes of some projective space , refining the Chow variety. The Hilbert scheme is a disjoint union of projective subschemes corresponding to Hilbert polynomials...
s, which were used to prove several conjectures made by Macdonald about them.
Definition
First fix some notation:- R is a finite root systemRoot systemIn mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
in a real vector space V. - R+ is a choice of positive roots, to which corresponds a positive Weyl chamber.
- W is the Weyl groupWeyl groupIn mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of R. - Q is the root lattice of R (the lattice spanned by the roots).
- P is the weight lattice of R (containing Q).
- An ordering on the weights:
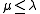if and only if 
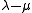is a nonnegative linear combination of simple roots. - P+ is the set of dominant weights: the elements of P in the positive Weyl chamber.
- ρ is the Weyl vector: half the sum of the positive roots; this is a special element of P+ in the interior of the positive Weyl chamber.
- F is a field of characteristic 0, usually the rational numbers.
- A = F(P) is the group algebraGroup algebraIn mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
of P, with a basis of elements written eλ for λ ∈ P. - If f = eλ, then f means e−λ, and this is extended by linearity to the whole group algebra.
- mμ = Σλ ∈ Wμeλ is an orbit sum; these elements form a basis for the subalgebra AW of elements fixed by W.
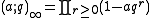, the infinite q-Pochhammer symbol.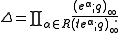
is the inner product of two elements of A, at least when t is a positive integer power of q.
The Macdonald polynomials Pλ for λ ∈ P+ are uniquely defined by the following two conditions:
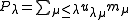where uλμ is a rational function of q and t with uλλ = 1;
- Pλ and Pμ are orthogonal if λ < μ.
In other words the Macdonald polynomials are obtained by orthogonalizing the obvious basis for AW. The existence of polynomials with these properties is easy to show (for any inner product). A key property of the Macdonald polynomials is that they are orthogonal: 〈Pλ, Pμ〉 = 0 whenever λ ≠ μ. This is not a trivial consequence of the definition because P+ is not totally ordered, so has plenty of elements that are incomparable, and one has to check that the corresponding polynomials are still orthogonal. The orthogonality can be proved by showing that the Macdonald polynomials are eigenvectors
for an algebra of commuting self adjoint operators with 1-dimensional eigenspaces, and using the fact that eigenspaces for different eigenvalues must be orthogonal.
In the case of non-simply-laced root systems (B, C, F, G), the parameter t can be chosen to vary with the length of the root, giving a three-parameter family of Macdonald polynomials. One can also extend the definition to the nonreduced root system BC, in which case one obtains a six-parameter family (one t for each orbit of roots, plus q) known as Koornwinder polynomials
Koornwinder polynomials
In mathematics, Koornwinder polynomials are a family of orthogonal polynomials in several variables, introduced by , that generalize the Askey-Wilson polynomials...
. It is sometimes better to regard Macdonald polynomials as depending on a possibly non-reduced affine root system. In this case there is one parameter t associated to each orbit of roots in the affine root system, plus one parameter q. The number of orbits of roots can vary from 1 to 5.
Examples
- If q = t the Macdonald polynomials become the Weyl characters of the representations of the compact group of the root system, or the Schur functions in the case of root systems of type A.
- If q = 0 the Macdonald polynomials become the (rescaled) zonal spherical functionZonal spherical functionIn mathematics, a zonal spherical function or often just spherical function is a function on a locally compact group G with compact subgroup K that arises as the matrix coefficient of a K-invariant vector in an irreducible representation of G...
s for a semisimple p-adic group, or the Hall–Littlewood polynomials when the root system has type A. - If t=1 the Macdonald polynomials become the sums over W orbits, which are the monomial symmetric functions when the root system has type A.
- If we put t = qα and let q tend to 1 the Macdonald polynomials become Jack polynomials when the root system is of type A, and Heckman–Opdam polynomialsHeckman–Opdam polynomialsIn mathematics, Heckman–Opdam polynomials Pλ are orthogonal polynomials in several variables associated to root systems...
for more general root systems. - For the affine root system A1, the Macdonald polynomials are the Rogers polynomialsRogers polynomialsIn mathematics, the Rogers polynomials, also called Rogers–Askey–Ismail polynomials and continuous q-ultraspherical polynomials, are a family of orthogonal polynomials introduced by in the course of his work on the Rogers–Ramanujan identities...
. - For the non-reduced rank 1 affine root system of type (C, C1), the Macdonald polynomials are the Askey–Wilson polynomialsAskey–Wilson polynomialsIn mathematics, the Askey–Wilson polynomials are a family of orthogonal polynomials introduced by as q-analogs of the Wilson polynomials. They include many of the other orthogonal polynomials in 1 variable as special or limiting cases, described in the Askey scheme...
, which in turn include as special cases most of the named families of orthogonal polynomials in 1 variable. - For the non-reduced affine root system of type (C, Cn), the Macdonald polynomials are the
Koornwinder polynomials
Koornwinder polynomials
In mathematics, Koornwinder polynomials are a family of orthogonal polynomials in several variables, introduced by , that generalize the Askey-Wilson polynomials...
.
The Macdonald constant term conjecture
If t = qk for some positive integer k, then the norm of the Macdonald polynomials is given by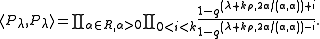This was conjectured by Macdonald (1982) as a generalization of the Dyson conjecture
Dyson conjecture
In mathematics, the Dyson conjecture is a conjecture about the constant term of certain Laurent polynomials, proved by Wilson and Gunson. Andrews generalized it to the q-Dyson conjecture, proved by Zeilberger and Bressoud and sometimes called the Zeilberger–Bressoud theorem...
, and proved for all (reduced) root systems by Cherednik (1995) using properties of double affine Hecke algebra
Double affine Hecke algebra
In mathematics, a double affine Hecke algebra, or Cherednik algebra, is an algebra containing the Hecke algebra of an affine Weyl group, given as the quotient of the group ring of a double affine braid group. They were introduced by Cherednik, who used them to prove Macdonald's constant term...
s. The conjecture had previously been proved case-by-case for all roots systems except those of type En by several authors.
There are two other conjectures which together with the norm conjecture are collectively referred to as the Macdonald conjectures in this context: in addition to the formula for the norm, Macdonald conjectured a formula for the value of Pλ at the point tρ, and a symmetry
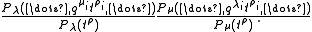
Again, these were proved for general reduced root systems by , using double affine Hecke algebra
Double affine Hecke algebra
In mathematics, a double affine Hecke algebra, or Cherednik algebra, is an algebra containing the Hecke algebra of an affine Weyl group, given as the quotient of the group ring of a double affine braid group. They were introduced by Cherednik, who used them to prove Macdonald's constant term...
s, with the extension to the BC case following shortly thereafter via work of van Diejen, Noumi, and Sahi.
The Macdonald positivity conjecture
In the case of roots systems of type An−1 the Macdonald polynomialscan be identified with symmetric polynomials in n variables (with coefficients that are rational functions of q and t). They can be expanded in terms of Schur functions, and the coefficients Kλμ(q,t) of these expansions are called Kostka–Macdonald coefficients.
Macdonald conjectured that the Kostka–Macdonald coefficients were polynomials in q and t with non-negative integer coefficients. These conjectures are now proved; the hardest and final step was proving the positivity, which was done by Mark Haiman
Mark Haiman
Mark David Haiman is a mathematician at the University of California at Berkeley who proved theMacdonald positivity conjecture for Macdonald polynomials.-References:* Haiman's *Mark Haiman J. Amer. Math. Soc. 14 , 941–1006...
(2001), by proving the n! conjecture.
n! conjecture
The n! conjecture of Adriano GarsiaAdriano Garsia
Adriano Mario Garsia is an Italian American mathematician, a leading expert in combinatorics, representation theory, and algebraic geometry, a student of Charles Loewner. He has made many deep contributions to representation theory, symmetric functions and algebraic combinatorics, which exerted a...
and Mark Haiman
Mark Haiman
Mark David Haiman is a mathematician at the University of California at Berkeley who proved theMacdonald positivity conjecture for Macdonald polynomials.-References:* Haiman's *Mark Haiman J. Amer. Math. Soc. 14 , 941–1006...
states that for each partition μ of n the space
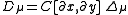
spanned by all higher partial derivatives of
has dimension n!, where (pj, qj) run through the n elements of the diagram of the partition μ, regarded as a subset of the pairs of non-negative integers.
For example, if μ is the partition 3 = 2 + 1 of n = 3 then the pairs (pj, qj) are
(0, 0), (0, 1), (1, 0), and the space Dμ is spanned by
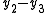
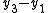
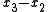
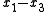
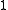
which has dimension 6 = 3
Haiman's proof of the Macdonald positivity conjecture and the n! conjecture involved showing that the isospectral Hilbert scheme of n points in a plane was Cohen–Macaulay (and even Gorenstein
Gorenstein ring
In commutative algebra, a Gorenstein local ring is a Noetherian commutative local ring R with finite injective dimension, as an R-module. There are many equivalent conditions, some of them listed below, most dealing with some sort of duality condition....
). Earlier results of Haiman and Garsia had already shown that this implied the n! conjecture, and that the n! conjecture implied that the Kostka–Macdonald coefficients were graded character multiplicities for the modules Dμ. This immediately implies the Macdonald positivity conjecture because character multiplicities have to be non-negative integers.
Ian Grojnowski and Mark Haiman found another proof of the Macdonald positivity conjecture by proving a positivity conjecture for LLT polynomial
LLT polynomial
In mathematics, an LLT polynomial is one of a family of symmetric functions introduced by Alain Lascoux, Bernard Leclerc, and Jean-Yves Thibon as q-analogues of products of Schur functions....
s.
External links
- Garsia's page about Macdonald polynomials.
- Some of Haiman's papers about Macdonald polynomials.