Affine Hecke algebra
Encyclopedia
In mathematics, an affine Hecke algebra is the Hecke algebra
of an affine Weyl group, and can be used to prove Macdonald's constant term conjecture for Macdonald polynomial
s.
be a Euclidean space of a finite dimension and 
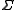an affine root system
on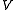
. An affine Hecke algebra is a certain associative algebra
that deforms the group algebra
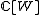of the Weyl group
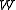of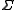 
(the affine Weyl group). It is usually denoted by 
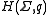, where 
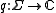is multiplicity function
that plays the role of deformation parameter. For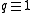
the affine Hecke algebra 
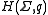indeed reduces to 
.
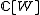introduced generalizations of affine Hecke algebras, the so-called double affine Hecke algebra
(usually referred to as DAHA). Using this he was able to give a proof of Macdonald's constant term conjecture for Macdonald polynomial
s (building on work of Eric Opdam). Another main inspiration for Cherednik to consider the double affine Hecke algebra was the quantum KZ equations
.
Hecke algebra
In mathematics, the Iwahori–Hecke algebra, or Hecke algebra, named for Erich Hecke and Nagayoshi Iwahori, is a one-parameter deformation of the group algebra of a Coxeter group....
of an affine Weyl group, and can be used to prove Macdonald's constant term conjecture for Macdonald polynomial
Macdonald polynomial
In mathematics, Macdonald polynomials Pλ are a family of orthogonal polynomials in several variables, introduced by...
s.
Definition
Let be a Euclidean space of a finite dimension and 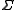an affine root systemAffine root system
In mathematics, an affine root system is a root system of affine-linear functions on a Euclidean space. They are used in the classification of affine Lie algebras and superalgebras, and semisimple p-adic algebraic groups, and correspond to families of Macdonald polynomials. The reduced affine root...
on
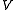. An affine Hecke algebra is a certain associative algebraAssociative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
that deforms the group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
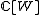of the Weyl groupWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
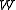of 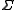(the affine Weyl group). It is usually denoted by 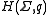, where 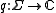is multiplicity functionMultiplicity function
The multiplicity function for a two state paramagnet, W, is the number of spin states such that n of the N spins point in the z-direction. This function is given by the combinatoric function C...
that plays the role of deformation parameter. For
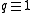the affine Hecke algebra 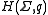indeed reduces to 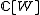.Generalizations
Ivan CherednikIvan Cherednik
Ivan Cherednik is a Russian mathematician. He introduced double affine Hecke algebras, and used them to prove Macdonald's constant term conjecture in . He has also dealt with algebraic geometry, number theory and Soliton equations. His research interests include representation theory,...
introduced generalizations of affine Hecke algebras, the so-called double affine Hecke algebra
Double affine Hecke algebra
In mathematics, a double affine Hecke algebra, or Cherednik algebra, is an algebra containing the Hecke algebra of an affine Weyl group, given as the quotient of the group ring of a double affine braid group. They were introduced by Cherednik, who used them to prove Macdonald's constant term...
(usually referred to as DAHA). Using this he was able to give a proof of Macdonald's constant term conjecture for Macdonald polynomial
Macdonald polynomial
In mathematics, Macdonald polynomials Pλ are a family of orthogonal polynomials in several variables, introduced by...
s (building on work of Eric Opdam). Another main inspiration for Cherednik to consider the double affine Hecke algebra was the quantum KZ equations
Quantum KZ equations
In mathematical physics, the quantum KZ equations or quantum Knizhnik–Zamolodchikov equations or qKZ equations are the analogue for quantum affine algebras of the Knizhnik–Zamolodchikov equations for affine Kac–Moody algebras. They are a consistent system of difference equations satisfied by the...
.