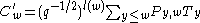Hecke algebra
Encyclopedia
In mathematics, the Iwahori–Hecke algebra, or Hecke algebra, named for Erich Hecke
and Nagayoshi Iwahori
, is a one-parameter deformation of the group algebra
of a Coxeter group
.
Hecke algebras are quotients of the group rings of Artin braid groups. This connection found a spectacular application in Vaughan Jones
' construction of new invariants of knots. Representations of Hecke algebras led to discovery of quantum group
s by Michio Jimbo
. Michael Freedman
proposed Hecke algebras as a foundation for topological quantum computation
.
Suppose for the following definitions that (W,S) is a Coxeter system with the Coxeter matrix M and R is a commutative ring with identity.
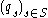is a family of units of 
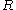such that 
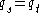whenever 
and 
are conjugate in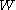 
, then define the multiparameter Hecke algebra 
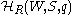as the unital, associative 
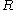-algebra with generators 
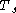for all 
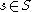and the relations:
If
is the ring 
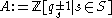of Laurent Polynomials over 
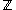with indeterminants 
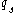(and the above restriction that 
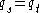whenever 
and 
are conjugated), then one calls the above Hecke algebra the generic multiparameter Hecke algebra.
The generic algebra is universal in the sense that every other multiparameter Hecke algebra can be obtained from it via the (unique) ring homomorphism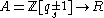
which maps the indeterminant 
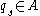to the unit 
. This homomorphism turns 
into a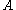 
-algebra and the scalar extension
is canonically isomorphic to the Hecke algebra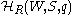
as constructed above. One calls this process specialization of the generic algebra.
Warning: in recent books and papers, Lusztig has been using a modified form of the quadratic relation that reads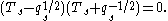
After extending the scalars to include the half integer powers 
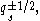the resulting Hecke algebra is isomorphic to the previously defined one (but the 
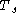here corresponds to 
in our notation). While this does not change the general theory, many formulas look different.
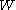(i.e. a map 
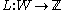with 
for all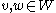 
with 
), then a common specialization to look at is the one induced by the homomorphism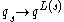 
, where 
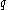is a single indeterminant over 
.
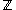If one uses the convention with half-integer powers, then weight function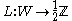
may be permitted as well. For technical reasons it is also often convenient only to consider positive weight functions.
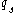to a single indeterminant 
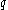over the integers (or 
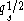to 
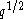respectively), then one obtains the so called generic one-parameter Hecke algebra of 
.
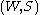Since in Coxeter groups with single laced Dynkin diagrams (for example groups of type A and D) every pair of Coxeter generators is conjugated, the above mentioned restriction of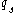
being equal 
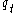whenever 
and 
are conjugated in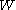 
forces the multiparameter and the one-parameter Hecke algebras to be equal. Therefore it is also very common to only look at one-parameter Hecke algebras.
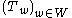over 
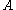indexed by the elements of the Coxeter group 
. In particular, 
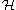is a free 
-module. If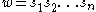 
is a reduced decomposition of 
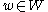, then 
. This basis of Hecke algebra is sometimes called the natural basis. The neutral element of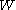 
corresponds to the identity of 
: 
.
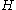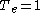2. The elements of the natural basis are multiplicative, namely,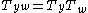
whenever 
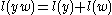, where 
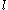denotes the length function
on the Coxeter group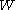
.
3. Elements of the natural basis are invertible. For example, from the quadratic relation we conclude that
.
4. Suppose that
is a finite group and the ground ring is the field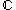 
of complex numbers. Jacques Tits
has proved that if the indeterminate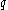
is specialized to any complex number outside of an explicitly given list (consisting of roots of unity), then the resulting one parameter Hecke algebra is semisimple
and isomorphic to the complex group algebra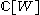
(which also corresponds to the specialization 
).
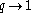5. More generally, if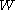
is a finite group and the ground ring 
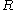is a field of characteristic zero, then the one parameter Hecke algebra is a semisimple associative algebra
over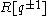
. Moreover, extending earlier results of Benson and Curtis, George Lusztig provided an explicit isomorphism between the Hecke algebra and the group algebra after the extension of scalars to the quotient field of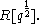 
Consider a Hecke algebra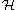
over the ring 
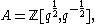as above. This ring has an involution bar that maps 
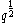to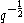
and acts as identity on 
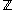. Then 
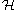admits a unique ring automorphism 
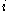that is semilinear
with respect to the bar involution of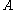
and maps 
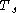to 
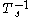. It can further be proved that this automorphism is involutive (has order two) and takes any 
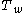to 
there exists a unique element 
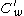which is invariant under the involution 
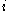and has the property that in the expansion
over the elements of the natural basis, one has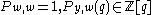
has degree 
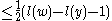if 
in the Bruhat order
and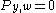
if 
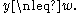
The elements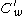
where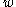 
varies over 
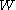form a basis of the algebra 
, which is called the dual canonical basis of the Hecke algebra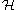 
. The canonical basis 
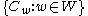is obtained in a similar way. The polynomials 
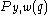making appearance in this theorem are the Kazhdan–Lusztig polynomials.
The Kazhdan–Lusztig notions of left, right and two-sided cells in Coxeter groups are defined through the behavior of the canonical basis under the action of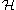
.
s of compact support
can be endowed with a structure of an associative algebra under the operation of convolution
. This algebra is denoted
and called the Hecke ring of the pair (G,K). If we start with a Gelfand pair
then the resulting algebra turns out to be commutative. In particular, this holds when
'
and the representations of the corresponding commutative Hecke ring were studied by Ian G. Macdonald
.
On the other hand, in the case
we arrive at the abstract ring behind Hecke operators in the theory of modular forms, which gave the name to Hecke algebras in general.
The case leading to the Hecke algebra of a finite Weyl group is when G is the finite Chevalley group over a finite field
with pk elements, and B is its Borel subgroup
. Iwahori showed that the Hecke ring
is obtained from the generic Hecke algebra Hq of the Weyl group
W of G by specializing the indeterminate q of the latter algebra to pk, the cardinality of the finite field. George Lusztig remarked in 1984 (Characters of reductive groups over a finite field, xi, footnote):
Iwahori and Matsumoto (1965) considered the case when G is a group of points of a reductive algebraic group over a non-archimedean local field
K, such as Qp, and K is what is now called an Iwahori subgroup
of G. The resulting Hecke ring is isomorphic to the Hecke algebra of the affine Weyl group of G, or the affine Hecke algebra
, where the indeterminate q has been specialized to the cardinality of the residue field
of K.
Work of Roger Howe in the 1970s and his papers with Allen Moy on representations of p-adic GLn opened a possibility of classifying irreducible admissible representations of reductive groups over local fields in terms of appropriately constructed Hecke algebras. (Important contributions were also made by Joseph Bernstein and Andrey Zelevinsky.) These ideas were taken much further in Colin Bushnell and Philip Kutzko's theory of types, allowing them to complete the classification in the general linear case. Many of the techniques can be extended to other reductive groups, which remains an area of active research. It has been conjectured that all Hecke algebras that are ever needed are mild generalizations of affine Hecke algebras.
s of finite Chevalley groups.
George Lusztig pushed this connection much further and was able to describe most of the characters of finite groups of Lie type in terms of representation theory of Hecke algebras. This work used a mixture of geometric techniques and various reductions, led to introduction of various objects generalizing Hecke algebras and detailed understanding of their representations (for q not a root of unity). Modular representations of Hecke algebras and representations at roots of unity turned out to be related with the theory of canonical bases in affine quantum groups and very interesting combinatorics.
Representation theory of affine Hecke algebras was developed by Lusztig with a view towards applying it to description of representations of p-adic groups. It is in many ways quite different in flavor from the finite case. A generalization of affine Hecke algebras, called double affine Hecke algebra, was used by Ivan Cherednik
in his proof of the Macdonald conjectures.
Erich Hecke
Erich Hecke was a German mathematician. He obtained his doctorate in Göttingen under the supervision of David Hilbert. Kurt Reidemeister and Heinrich Behnke were among his students....
and Nagayoshi Iwahori
Nagayoshi Iwahori
Nagayoshi Iwahori is a Japanese mathematician working on algebraic groups over local fields who introduced Iwahori–Hecke algebras and Iwahori subgroups....
, is a one-parameter deformation of the group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
of a Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
.
Hecke algebras are quotients of the group rings of Artin braid groups. This connection found a spectacular application in Vaughan Jones
Vaughan Jones
Sir Vaughan Frederick Randal Jones, KNZM, FRS, FRSNZ is a New Zealand mathematician, known for his work on von Neumann algebras, knot polynomials and conformal field theory. He was awarded a Fields Medal in 1990, and famously wore a New Zealand rugby jersey when he accepted the prize...
' construction of new invariants of knots. Representations of Hecke algebras led to discovery of quantum group
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
s by Michio Jimbo
Michio Jimbo
is a Japanese mathematician, currently a professor at the University of Tokyo. He is a grandson of the linguist Kaku Jimbo.After graduating from the University of Tokyo in 1974, he studied under Mikio Sato at the Research Institute for Mathematical Sciences in Kyoto University...
. Michael Freedman
Michael Freedman
Michael Hartley Freedman is a mathematician at Microsoft Station Q, a research group at the University of California, Santa Barbara. In 1986, he was awarded a Fields Medal for his work on the Poincaré conjecture. Freedman and Robion Kirby showed that an exotic R4 manifold exists.Freedman was born...
proposed Hecke algebras as a foundation for topological quantum computation
Topological quantum computer
A topological quantum computer is a theoretical quantum computer that employs two-dimensional quasiparticles called anyons, whose world lines cross over one another to form braids in a three-dimensional spacetime . These braids form the logic gates that make up the computer...
.
Definitions
There are several definitions of Hecke algebras in the literature which are more or less general.Suppose for the following definitions that (W,S) is a Coxeter system with the Coxeter matrix M and R is a commutative ring with identity.
Multiparameter Hecke algebras
If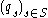 is a family of units of 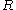such that 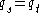whenever and are conjugate in 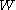, then define the multiparameter Hecke algebra 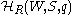as the unital, associative 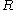-algebra with generators 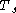for all 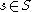and the relations:
-
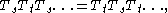where each side has 
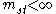factors and 
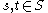(braid relations) -
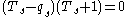for all 
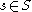(quadratic relation).
If
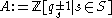is the ring of Laurent Polynomials over 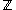with indeterminants 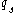(and the above restriction that 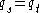whenever and are conjugated), then one calls the above Hecke algebra the generic multiparameter Hecke algebra.The generic algebra is universal in the sense that every other multiparameter Hecke algebra can be obtained from it via the (unique) ring homomorphism
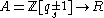which maps the indeterminant 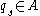to the unit . This homomorphism turns into a 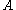-algebra and the scalar extensionis canonically isomorphic to the Hecke algebra
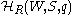as constructed above. One calls this process specialization of the generic algebra.Warning: in recent books and papers, Lusztig has been using a modified form of the quadratic relation that reads
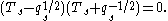After extending the scalars to include the half integer powers 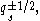the resulting Hecke algebra is isomorphic to the previously defined one (but the 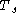here corresponds to in our notation). While this does not change the general theory, many formulas look different.Coxeter groups with weights
If an integral weight function is defined on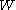 (i.e. a map 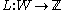with for all 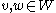with ), then a common specialization to look at is the one induced by the homomorphism 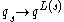, where 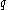is a single indeterminant over 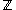.If one uses the convention with half-integer powers, then weight function
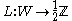may be permitted as well. For technical reasons it is also often convenient only to consider positive weight functions.One-parameter Hecke algebras
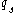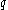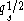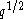If one specializes every indeterminant to a single indeterminant over the integers (or to respectively), then one obtains the so called generic one-parameter Hecke algebra of 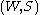.Since in Coxeter groups with single laced Dynkin diagrams (for example groups of type A and D) every pair of Coxeter generators is conjugated, the above mentioned restriction of
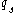being equal 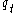whenever and are conjugated in 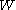forces the multiparameter and the one-parameter Hecke algebras to be equal. Therefore it is also very common to only look at one-parameter Hecke algebras.Properties
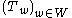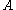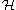1. The Hecke algebra has a basis over indexed by the elements of the Coxeter group . In particular, is a free -module. If 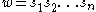is a reduced decomposition of 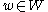, then . This basis of Hecke algebra is sometimes called the natural basis. The neutral element of 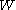corresponds to the identity of 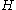: 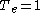.2. The elements of the natural basis are multiplicative, namely,
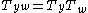whenever 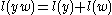, where 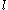denotes the length functionLength function
In mathematical field of geometric group theory, a length function is a function that assigns a number to each element of a group.-Definition:...
on the Coxeter group
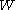.3. Elements of the natural basis are invertible. For example, from the quadratic relation we conclude that
.4. Suppose that
is a finite group and the ground ring is the field 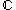of complex numbers. Jacques TitsJacques Tits
Jacques Tits is a Belgian and French mathematician who works on group theory and geometry and who introduced Tits buildings, the Tits alternative, and the Tits group.- Career :Tits received his doctorate in mathematics at the age of 20...
has proved that if the indeterminate
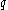is specialized to any complex number outside of an explicitly given list (consisting of roots of unity), then the resulting one parameter Hecke algebra is semisimpleSemisimple
In mathematics, the term semisimple is used in a number of related ways, within different subjects. The common theme is the idea of a decomposition into 'simple' parts, that fit together in the cleanest way...
and isomorphic to the complex group algebra
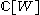(which also corresponds to the specialization 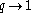).5. More generally, if
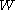is a finite group and the ground ring 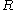is a field of characteristic zero, then the one parameter Hecke algebra is a semisimple associative algebraSemisimple algebra
In ring theory, a semisimple algebra is an associative algebra which has trivial Jacobson radical...
over
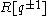. Moreover, extending earlier results of Benson and Curtis, George Lusztig provided an explicit isomorphism between the Hecke algebra and the group algebra after the extension of scalars to the quotient field of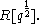 Canonical basis
A great discovery of Kazhdan and Lusztig was that a Hecke algebra admits a different basis, which in a way controls representation theory of a variety of related objects.Consider a Hecke algebra
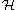over the ring 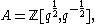as above. This ring has an involution bar that maps 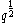to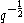 and acts as identity on 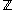. Then 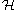admits a unique ring automorphism 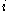that is semilinearSemilinear transformation
In linear algebra, particularly projective geometry, a semilinear transformation between vector spaces V and W over a field K is a function that is a linear transformation "up to a twist", hence semi-linear, where "twist" means "field automorphism of K"...
with respect to the bar involution of
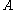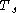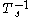and maps to . It can further be proved that this automorphism is involutive (has order two) and takes any 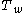to Theorem (Kazhdan–Lusztig)
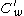For each there exists a unique element which is invariant under the involution 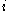and has the property that in the expansion
over the elements of the natural basis, one has
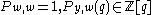has degree 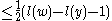if in the Bruhat orderBruhat order
In mathematics, the Bruhat order is a partial order on the elements of a Coxeter group, that corresponds to the inclusion order on Schubert varieties.-History:The Bruhat order on the Schubert varieties of a flag manifold or Grassmannian...
and
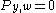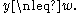
if The elements
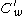where 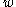varies over 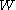form a basis of the algebra , which is called the dual canonical basis of the Hecke algebra 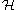. The canonical basis 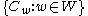is obtained in a similar way. The polynomials 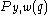making appearance in this theorem are the Kazhdan–Lusztig polynomials.The Kazhdan–Lusztig notions of left, right and two-sided cells in Coxeter groups are defined through the behavior of the canonical basis under the action of
.Hecke algebra of a locally compact group
Iwahori–Hecke algebras first appeared as an important special case of a very general construction in group theory. Let (G,K) be a pair consisting of a unimodular locally compact topological group G and a closed subgroup K of G. Then the space of bi-K-invariant continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s of compact support
- C[K\G/K]
can be endowed with a structure of an associative algebra under the operation of convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
. This algebra is denoted
- H(G//K)
and called the Hecke ring of the pair (G,K). If we start with a Gelfand pair
Gelfand pair
In mathematics, the expression Gelfand pair is a pair consisting of a group G and a subgroup K that satisfies a certain property on restricted representations. The theory of Gelfand pairs is closely related to the topic of spherical functions in the classical theory of special functions, and to...
then the resulting algebra turns out to be commutative. In particular, this holds when
'
- G = SLn(Qp) and K = SLn(Zp)
and the representations of the corresponding commutative Hecke ring were studied by Ian G. Macdonald
Ian G. Macdonald
Ian Grant Macdonald is a British mathematician known for his contributions to symmetric functions, special functions, Lie algebra theory and other aspects of algebraic combinatorics ....
.
On the other hand, in the case
- G = SL2(Q) and K = SL2(Z)
we arrive at the abstract ring behind Hecke operators in the theory of modular forms, which gave the name to Hecke algebras in general.
The case leading to the Hecke algebra of a finite Weyl group is when G is the finite Chevalley group over a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with pk elements, and B is its Borel subgroup
Borel subgroup
In the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
. Iwahori showed that the Hecke ring
- H(G//B)
is obtained from the generic Hecke algebra Hq of the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
W of G by specializing the indeterminate q of the latter algebra to pk, the cardinality of the finite field. George Lusztig remarked in 1984 (Characters of reductive groups over a finite field, xi, footnote):
- I think it would be most appropriate to call it the Iwahori algebra, but the name Hecke ring (or algebra) given by Iwahori himself has been in use for almost 20 years and it is probably too late to change it now.
Iwahori and Matsumoto (1965) considered the case when G is a group of points of a reductive algebraic group over a non-archimedean local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
K, such as Qp, and K is what is now called an Iwahori subgroup
Iwahori subgroup
In algebra, an Iwahori subgroup is a subgroup of a reductive algebraic group over a local field that is analogous to a Borel subgroup of an algebraic group. A parahoric subgroup is a subgroup that is a finite union of double cosets of an Iwahori subgroup, so is analogous to a parabolic subgroup of...
of G. The resulting Hecke ring is isomorphic to the Hecke algebra of the affine Weyl group of G, or the affine Hecke algebra
Affine Hecke algebra
In mathematics, an affine Hecke algebra is the Hecke algebra of an affine Weyl group, and can be used to prove Macdonald's constant term conjecture for Macdonald polynomials.-Definition:...
, where the indeterminate q has been specialized to the cardinality of the residue field
Residue field
In mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
of K.
Work of Roger Howe in the 1970s and his papers with Allen Moy on representations of p-adic GLn opened a possibility of classifying irreducible admissible representations of reductive groups over local fields in terms of appropriately constructed Hecke algebras. (Important contributions were also made by Joseph Bernstein and Andrey Zelevinsky.) These ideas were taken much further in Colin Bushnell and Philip Kutzko's theory of types, allowing them to complete the classification in the general linear case. Many of the techniques can be extended to other reductive groups, which remains an area of active research. It has been conjectured that all Hecke algebras that are ever needed are mild generalizations of affine Hecke algebras.
Representations of Hecke algebras
It follows from Iwahori's work that complex representations of Hecke algebras of finite type are intimately related with the structure of the spherical principal series representationPrincipal series representation
In mathematics, the principal series representations of certain kinds of topological group G occur in the case where G is not a compact group. There, by analogy with spectral theory, one expects that the regular representation of G will decompose according to some kind of continuous spectrum, of...
s of finite Chevalley groups.
George Lusztig pushed this connection much further and was able to describe most of the characters of finite groups of Lie type in terms of representation theory of Hecke algebras. This work used a mixture of geometric techniques and various reductions, led to introduction of various objects generalizing Hecke algebras and detailed understanding of their representations (for q not a root of unity). Modular representations of Hecke algebras and representations at roots of unity turned out to be related with the theory of canonical bases in affine quantum groups and very interesting combinatorics.
Representation theory of affine Hecke algebras was developed by Lusztig with a view towards applying it to description of representations of p-adic groups. It is in many ways quite different in flavor from the finite case. A generalization of affine Hecke algebras, called double affine Hecke algebra, was used by Ivan Cherednik
Ivan Cherednik
Ivan Cherednik is a Russian mathematician. He introduced double affine Hecke algebras, and used them to prove Macdonald's constant term conjecture in . He has also dealt with algebraic geometry, number theory and Soliton equations. His research interests include representation theory,...
in his proof of the Macdonald conjectures.