
Koornwinder polynomials
Encyclopedia
In mathematics, Koornwinder polynomials (also called Macdonald-Koornwinder polynomials) are a family of orthogonal polynomials
in several variables, introduced by , that generalize the Askey-Wilson polynomials. They are the Macdonald polynomials attached to the non-reduced affine root system of type (C, Cn), and in particular satisfy analogues of Macdonald's conjectures . In addition Jan Felipe van Diejen showed that the Macdonald polynomials associated to any classical root system can be expressed as limits or special cases of Koornwinder polynomials and found complete sets of concrete commuting difference operators diagonalized by them . Furthermore there is a large class of interesting families of multivariable orthogonal polynomials associated with classical root systems which are degenerate cases of the Koornwinder-Macdonald polynomials . The Koornwinder-Macdonald polynomials have also been studied with the aid of affine Hecke algebra
s .
The Koornwinder polynomial in n variables associated to the partition λ is the unique Laurent polynomial invariant under permutation and inversion of variables, with leading monomial xλ, and orthogonal with respect to the density
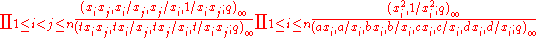
on the unit torus
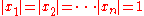 ,
,
where the parameters satisfy the constraints
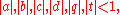
and (x;q)∞ denotes the infinite q-Pochhammer symbol.
Here leading monomial xλ means that μ≤λ for all terms xμ with nonzero coefficient, where μ≤λ if and only if μ1≤λ1, μ1+μ2≤λ1+λ2, …, μ1+…+μn≤λ1+…+λn.
Under further constraints that q and t are real and that a, b, c, d are real or, if complex, occur in conjugate pairs, the given density is positive.
For some lecture notes on Koornwinder polynomials from a Hecke algebra perspective see for example .
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
in several variables, introduced by , that generalize the Askey-Wilson polynomials. They are the Macdonald polynomials attached to the non-reduced affine root system of type (C, Cn), and in particular satisfy analogues of Macdonald's conjectures . In addition Jan Felipe van Diejen showed that the Macdonald polynomials associated to any classical root system can be expressed as limits or special cases of Koornwinder polynomials and found complete sets of concrete commuting difference operators diagonalized by them . Furthermore there is a large class of interesting families of multivariable orthogonal polynomials associated with classical root systems which are degenerate cases of the Koornwinder-Macdonald polynomials . The Koornwinder-Macdonald polynomials have also been studied with the aid of affine Hecke algebra
Affine Hecke algebra
In mathematics, an affine Hecke algebra is the Hecke algebra of an affine Weyl group, and can be used to prove Macdonald's constant term conjecture for Macdonald polynomials.-Definition:...
s .
The Koornwinder polynomial in n variables associated to the partition λ is the unique Laurent polynomial invariant under permutation and inversion of variables, with leading monomial xλ, and orthogonal with respect to the density
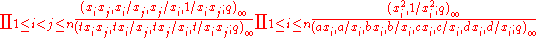
on the unit torus
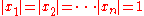 ,
,where the parameters satisfy the constraints
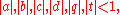
and (x;q)∞ denotes the infinite q-Pochhammer symbol.
Here leading monomial xλ means that μ≤λ for all terms xμ with nonzero coefficient, where μ≤λ if and only if μ1≤λ1, μ1+μ2≤λ1+λ2, …, μ1+…+μn≤λ1+…+λn.
Under further constraints that q and t are real and that a, b, c, d are real or, if complex, occur in conjugate pairs, the given density is positive.
For some lecture notes on Koornwinder polynomials from a Hecke algebra perspective see for example .

