
Gorenstein ring
Encyclopedia
In commutative algebra
, a Gorenstein local ring is a Noetherian
commutative local ring
R with finite injective dimension, as an R-module. There are many equivalent conditions, some of them listed below, most dealing with some sort of duality condition.
A Gorenstein commutative ring is a commutative ring such that each localization
at a prime ideal
is a Gorenstein local ring. The Gorenstein ring concept is a special case of the more general Cohen-Macaulay ring
.
The classical definition reads:
A local Cohen-Macaulay ring
R is called Gorenstein if there is a maximal R-regular sequence
in the maximal ideal generating an irreducible ideal
.
For a Noetherian
commutative local ring
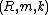 of Krull dimension
of Krull dimension  , the following are equivalent:
, the following are equivalent:
A (not necessarily commutative) ring R is called Gorenstein if R has finite injective dimension both as a left R-module and as a right R-module. If R is a local ring, we say R is a local Gorenstein ring.
A noteworthy occurrence of the concept is as one ingredient (among many) of
the solution by Andrew Wiles
to the Fermat Conjecture
.
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, a Gorenstein local ring is a Noetherian
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
commutative local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
R with finite injective dimension, as an R-module. There are many equivalent conditions, some of them listed below, most dealing with some sort of duality condition.
A Gorenstein commutative ring is a commutative ring such that each localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
at a prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
is a Gorenstein local ring. The Gorenstein ring concept is a special case of the more general Cohen-Macaulay ring
Cohen-Macaulay ring
In mathematics, a Cohen–Macaulay ring is a particular type of commutative ring, possessing some of the algebraic-geometric properties of a nonsingular variety, such as local equidimensionality....
.
The classical definition reads:
A local Cohen-Macaulay ring
Cohen-Macaulay ring
In mathematics, a Cohen–Macaulay ring is a particular type of commutative ring, possessing some of the algebraic-geometric properties of a nonsingular variety, such as local equidimensionality....
R is called Gorenstein if there is a maximal R-regular sequence
Regular sequence (algebra)
In commutative algebra, if R is a commutative ring and M an R-module, a nonzero element r in R is called M-regular if r is not a zerodivisor on M, and M/rM is nonzero...
in the maximal ideal generating an irreducible ideal
Irreducible ideal
In mathematics, an ideal of a commutative ring is said to be irreducible if it cannot be written as a finite intersection of ideals properly containing it....
.
For a Noetherian
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
commutative local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
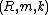 of Krull dimension
of Krull dimension  , the following are equivalent:
, the following are equivalent:
-
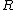 has finite injective dimension as an
has finite injective dimension as an 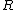 -module;
-module; -
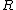 has injective dimension
has injective dimension  as an
as an 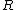 -module;
-module; -
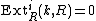 for
for 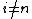 and
and  is isomorphic to
is isomorphic to 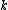 ;
; -
 for some
for some 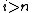 ;
; -
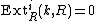 for all
for all 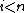 and
and 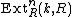 is isomorphic to
is isomorphic to 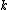 ;
; -
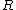 is an
is an  -dimensional Gorenstein ring.
-dimensional Gorenstein ring.
A (not necessarily commutative) ring R is called Gorenstein if R has finite injective dimension both as a left R-module and as a right R-module. If R is a local ring, we say R is a local Gorenstein ring.
A noteworthy occurrence of the concept is as one ingredient (among many) of
the solution by Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
to the Fermat Conjecture
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
.
Examples
- Every local complete intersection ring is Gorenstein.
- Every regular local ringRegular local ringIn commutative algebra, a regular local ring is a Noetherian local ring having the property that the minimal number of generators of its maximal ideal is equal to its Krull dimension. In symbols, let A be a Noetherian local ring with maximal ideal m, and suppose a1, ..., an is a minimal set of...
is a complete intersection ring, so is Gorenstein. - Every fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
is a regular local ring, so is Gorenstein.

