
Irreducible ideal
Encyclopedia
In mathematics
, an ideal
of a commutative ring
is said to be irreducible if it cannot be written as a finite intersection of ideals properly containing it.
Every prime ideal
is irreducible. Every irreducible ideal of a Noetherian ring
is a primary ideal
, and consequently for Noetherian rings an irreducible decomposition is a primary decomposition. Every primary ideal of a principal ideal domain
is an irreducible ideal. Every irreducible ideal is a primal ideal
.
An element of an integral domain is prime
if, and only if, an ideal generated by it is a nonzero prime ideal. This is not true for irreducible ideals: an irreducible ideal may be generated by an element that is not an irreducible element
, as is the case in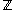 for the ideal
for the ideal 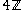 : It is not the intersection of two strictly greater ideals.
: It is not the intersection of two strictly greater ideals.
The notion is more easily understood in terms of algebraic geometry
. An ideal I of a ring A is irreducible if, and only if.the algebraic set
it defines is irreducible (that is, any open subset is dense) for the Zariski topology
, or equivalently if the closed space of spec
A consisting of prime ideals containing I is irreducible for the spectral topology.
If k is an algebraically closed field
, choosing the radical
of an irreducible ideal of a polynomial ring over k is the same thing as choosing an embedding
of the affine variety of its Nullstelle in the affine space.
See also: Laskerian ring, irreducible module, irreducible space
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
is said to be irreducible if it cannot be written as a finite intersection of ideals properly containing it.
Every prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
is irreducible. Every irreducible ideal of a Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
is a primary ideal
Primary ideal
In mathematics, specifically commutative algebra, a proper ideal Q of a commutative ring A is said to be primary if whenever xy is an element of Q then x or yn is also an element of Q, for some n...
, and consequently for Noetherian rings an irreducible decomposition is a primary decomposition. Every primary ideal of a principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
is an irreducible ideal. Every irreducible ideal is a primal ideal
Primal ideal
In mathematics, an element a of a commutative ring A is called prime to an ideal Q if whenever ab is an element of Q then b is also an element of Q....
.
An element of an integral domain is prime
Prime element
In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...
if, and only if, an ideal generated by it is a nonzero prime ideal. This is not true for irreducible ideals: an irreducible ideal may be generated by an element that is not an irreducible element
Irreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
, as is the case in
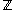 for the ideal
for the ideal 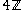 : It is not the intersection of two strictly greater ideals.
: It is not the intersection of two strictly greater ideals.The notion is more easily understood in terms of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. An ideal I of a ring A is irreducible if, and only if.the algebraic set
Algebraic set
In mathematics, an algebraic set over an algebraically closed field K is the set of solutions in Kn of a set of simultaneous equationsand so on up to...
it defines is irreducible (that is, any open subset is dense) for the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
, or equivalently if the closed space of spec
Spec
-Specification:* Specification , an explicit set of requirements to be satisfied by a material, product, or service** "Spec sheet" or datasheet used to describe something technical...
A consisting of prime ideals containing I is irreducible for the spectral topology.
If k is an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
, choosing the radical
Radical of an ideal
In commutative ring theory, a branch of mathematics, the radical of an ideal I is an ideal such that an element x is in the radical if some power of x is in I. A radical ideal is an ideal that is its own radical...
of an irreducible ideal of a polynomial ring over k is the same thing as choosing an embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
of the affine variety of its Nullstelle in the affine space.
See also: Laskerian ring, irreducible module, irreducible space

