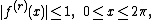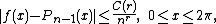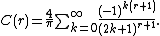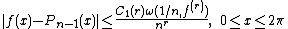In approximation theory

Approximation theory

In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...

, Jackson's inequality is an inequality bounding the value of function's best approximation by algebraic or trigonometric polynomials in terms of the modulus of continuity

Modulus of continuity

In mathematical analysis, a modulus of continuity is a function\omega:[0,\infty]\to[0,\infty]used to measure quantitatively the uniform continuity of functions. So, a function f:I\to\R admits \omega as a modulus of continuity if and only if|f-f|\leq\omega,for all x and y in the domain of f...

 of its derivatives. Informally speaking, the smoother the function is, the better it can be approximated by polynomials.

Statement: trigonometric polynomials

For trigonometric polynomials, the following was proved by Dunham Jackson

Dunham Jackson

Dunham Jackson was a mathematician who worked within approximation theory, notably with trigonometrical and orthogonal polynomials. He is known for Jackson's inequality. He was awarded the Chauvenet Prize in 1935...

:

Theorem 1: If ƒ: [0, 2] → C is an r times differentiable periodic function

Periodic function

In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...

 such that

then, for every natural n, there exists a trigonometric polynomial

Trigonometric polynomial

In the mathematical subfields of numerical analysis and mathematical analysis, a trigonometric polynomial is a finite linear combination of functions sin and cos with n a natural number. The coefficients may be taken as real numbers, for real-valued functions...

 P_n−1 of degree at most n − 1 such that

where C(r) depends only on r.

The Akhiezer–Krein–Favard

Jean Favard

Jean Favard was a French mathematician who worked on analysis.During World War II he was a prisoner of war in Germany.He also was a President of the French Mathematical Society in 1946....

 theorem gives the sharp value of C(r) (called the Akhiezer–Krein–Favard constant):

Jackson also proved the following generalisation of Theorem 1:

Theorem 2: Denote by ω(δ, ƒ^(r)) the modulus of continuity of the rth derivative of ƒ. Then one can find P_n−1 such that

Further remarks

Generalisations and extensions are called Jackson-type theorems. A converse to Jackson's inequality is given by Bernstein's theorem

Bernstein's theorem (approximation theory)

In approximation theory, Bernstein's theorem is a converse to Jackson's theorem. The first results of this type were proved by Sergei Bernstein in 1912.For approximation by trigonometric polynomials, the result is as follows:...

. See also constructive function theory

Constructive function theory

In mathematical analysis, constructive function theory is a field which studies the connection between the smoothness of a function and its degree of approximation. It is closely related to approximation theory. The term was coined by Sergei Bernstein....

.

External links

• Jackson inequality on Encyclopaedia of Mathematics.