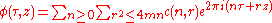Jacobi form
Encyclopedia
In mathematics, a Jacobi form is an automorphic form
on the Jacobi group
, which is the semidirect product
of the symplectic group
Sp(n;R) and the Heisenberg group .The theory was first systematically studied by .
.The theory was first systematically studied by .
s of genus 2. Examples with more than two variables include characters of some irreducible highest-weight representations of affine Kac–Moody algebra
s. Meromorphic Jacobi forms appear in the theory of Mock modular forms.
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
on the Jacobi group
Jacobi group
In mathematics, the Jacobi group, introduced by, is the semidirect product of the symplectic group Sp2n and the Heisenberg group R1+2n. The concept is name after Carl Gustav Jacob Jacobi. Automorphic forms on the Jacobi group are called Jacobi forms....
, which is the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of the symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
Sp(n;R) and the Heisenberg group
 .The theory was first systematically studied by .
.The theory was first systematically studied by .Definition
A Jacobi form of level 1, weight k and index m is a function φ(τ,z) of two complex variables (with τ in the upper half plane) such that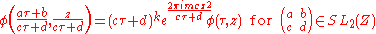
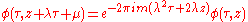 for all integers λ μ.
for all integers λ μ.- φ has a Fourier expansion
Examples
Examples in two variables include Jacobi theta functions, the Weierstrass ℘ function, and Fourier–Jacobi coefficients of Siegel modular formSiegel modular form
In mathematics, Siegel modular forms are a major type of automorphic form. These stand in relation to the conventional elliptic modular forms as abelian varieties do in relation to elliptic curves; the complex manifolds constructed as in the theory are basic models for what a moduli space for...
s of genus 2. Examples with more than two variables include characters of some irreducible highest-weight representations of affine Kac–Moody algebra
Kac–Moody algebra
In mathematics, a Kac–Moody algebra is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix...
s. Meromorphic Jacobi forms appear in the theory of Mock modular forms.