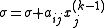Jacobi method
Encyclopedia
In numerical linear algebra
, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process is then iterated until it converges. This algorithm is a stripped-down version of the Jacobi transformation method of matrix diagonalization
. The method is named after German
mathematician Carl Gustav Jakob Jacobi
.
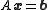
where:
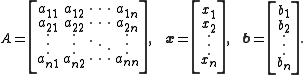
Then A can be decomposed into a diagonal
component D, and the remainder R:
The element-based formula is thus:
Note that the computation of xi(k+1) requires each element in x(k) except itself. Unlike the Gauss–Seidel method, we can't overwrite xi(k) with xi(k+1), as that value will be needed by the rest of the computation. The minimum amount of storage is two vectors of size n.
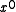to the solution
of the iteration matrix is less than 1:
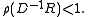
The method is guaranteed to converge if the matrix A is strictly or irreducibly diagonally dominant
. Strict row diagonal dominance means that for each row, the absolute value of the diagonal term is greater than the sum of absolute values of other terms:
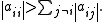
The Jacobi method sometimes converges even if these conditions are not satisfied.
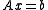with initial estimate 
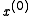is given by
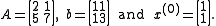
We use the equation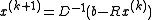
, described above, to estimate 
. First, we rewrite the equation in a more convenient form 
, where 
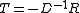and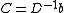 
. Note that 
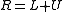where 
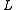and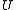 
are the strictly lower and upper parts of 
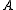. From the known values
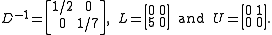
we determine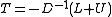
as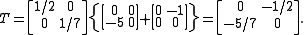
Further, C is found as
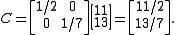
With T and C calculated, we estimate
as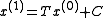 
:
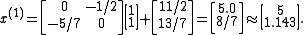
The next iteration yields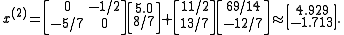
This process is repeated until convergence (i.e., until
is small). The solution after 25 iterations is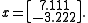
Numerical linear algebra
Numerical linear algebra is the study of algorithms for performing linear algebra computations, most notably matrix operations, on computers. It is often a fundamental part of engineering and computational science problems, such as image and signal processing, Telecommunication, computational...
, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process is then iterated until it converges. This algorithm is a stripped-down version of the Jacobi transformation method of matrix diagonalization
Jacobi eigenvalue algorithm
In numerical linear algebra, the Jacobi eigenvalue algorithm is an iterative method for the calculation of the eigenvalues and eigenvectors of a real symmetric matrix...
. The method is named after German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
mathematician Carl Gustav Jakob Jacobi
Carl Gustav Jakob Jacobi
Carl Gustav Jacob Jacobi was a German mathematician, widely considered to be the most inspiring teacher of his time and is considered one of the greatest mathematicians of his generation.-Biography:...
.
Description
Given a square system of n linear equations: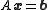where:
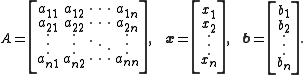
Then A can be decomposed into a diagonal
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
component D, and the remainder R:
The element-based formula is thus:
Note that the computation of xi(k+1) requires each element in x(k) except itself. Unlike the Gauss–Seidel method, we can't overwrite xi(k) with xi(k+1), as that value will be needed by the rest of the computation. The minimum amount of storage is two vectors of size n.
Algorithm
Choose an initial guess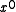 to the solution - while convergence not reached do
- for i := 1 step until n do
-
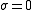
- for j := 1 step until n do
- if j != i then
-
- end if
- if j != i then
- end (j-loop)
-
-
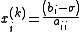
- end (i-loop)
- check if convergence is reached
- for i := 1 step until n do
- end (while convergence condition not reached loop)
Convergence
The standard convergence condition (for any iterative method) is when the spectral radiusSpectral radius
In mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
of the iteration matrix is less than 1:
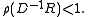
The method is guaranteed to converge if the matrix A is strictly or irreducibly diagonally dominant
Diagonally dominant matrix
In mathematics, a matrix is said to be diagonally dominant if for every row of the matrix, the magnitude of the diagonal entry in a row is larger than or equal to the sum of the magnitudes of all the other entries in that row...
. Strict row diagonal dominance means that for each row, the absolute value of the diagonal term is greater than the sum of absolute values of other terms:
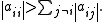
The Jacobi method sometimes converges even if these conditions are not satisfied.
Example
A linear system of the form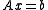 with initial estimate 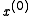is given by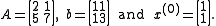We use the equation
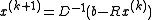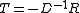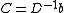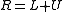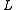, described above, to estimate . First, we rewrite the equation in a more convenient form , where and . Note that where and 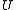are the strictly lower and upper parts of 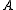. From the known values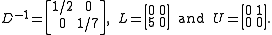we determine
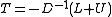as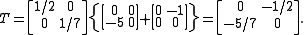Further, C is found as
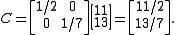
With T and C calculated, we estimate
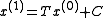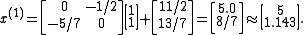
as :The next iteration yields
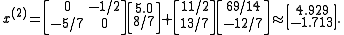
This process is repeated until convergence (i.e., until
is small). The solution after 25 iterations is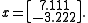See also
- Gauss–Seidel method
- Successive over-relaxationSuccessive over-relaxationIn numerical linear algebra, the method of successive over-relaxation is a variant of the Gauss–Seidel method for solving a linear system of equations, resulting in faster convergence. A similar method can be used for any slowly converging iterative process.It was devised simultaneously by David...
- Iterative method. Linear systems
- Gaussian Belief Propagation