
Diagonally dominant matrix
Encyclopedia
In mathematics, a matrix
is said to be diagonally dominant if for every row of the matrix, the magnitude of the diagonal entry in a row is larger than or equal to the sum of the magnitudes of all the other (non-diagonal) entries in that row. More precisely, the matrix A is diagonally dominant if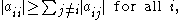
where aij denotes the entry in the ith row and jth column.
Note that this definition uses a weak inequality, and is therefore sometimes called weak diagonal dominance. If a strict inequality (>) is used, this is called strict diagonal dominance. The unqualified term diagonal dominance can mean both strict and weak diagonal dominance, depending on the context.
If an irreducible
matrix is weakly diagonally dominant, but in at least one row (or column) is strictly diagonally dominant, then the matrix is irreducibly diagonally dominant.
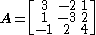
gives
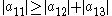 since
since 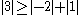
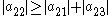 since
since 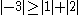
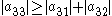 since
since 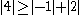 .
.
Because the magnitude of each diagonal element is greater than or equal to the sum of the magnitude of other elements in the row, A is diagonally dominant.
The matrix
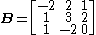
But here,
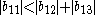 since
since 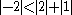
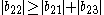 since
since 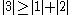
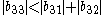 since
since 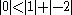 .
.
Because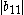 and
and 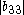 are less than the sum of the magnitude of other elements in their respective row, B is not diagonally dominant.
are less than the sum of the magnitude of other elements in their respective row, B is not diagonally dominant.
The matrix
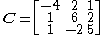
gives
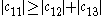 since
since 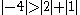
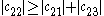 since
since 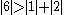
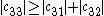 since
since 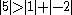 .
.
Because the magnitude of each diagonal element is greater than the sum of the magnitude of the other elements in the row, C is strictly diagonally dominant.
, a strictly (or irreducibly) diagonally dominant matrix is non-singular. This result is known as the Levy–Desplanques theorem.
A Hermitian diagonally dominant matrix with real non-negative diagonal entries is positive semi-definite. If the symmetry requirement is eliminated, such a matrix is not necessarily positive semi-definite; however, the real parts of its eigenvalues are non-negative.
No (partial) pivoting is necessary for a strictly column diagonally dominant matrix when performing Gaussian elimination
(LU factorization).
The Jacobi
and Gauss–Seidel methods for solving a linear system converge if the matrix is strictly (or irreducibly) diagonally dominant. In October 2010, researchers at Carnegie Mellon University
announced that they have discovered a new algorithm for solving symmetric diagonally dominant linear systems.
Many matrices that arise in finite element method
s are diagonally dominant.
A slight variation on the idea of diagonal dominance is used to prove that the pairing on diagrams without loops in the Temperley–Lieb algebra is nondegenerate. For a matrix with polynomial entries, one sensible definition of diagonal dominance is if the highest power of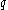 appearing in each row appears only on the diagonal. (The evaluations of such a matrix at large values of
appearing in each row appears only on the diagonal. (The evaluations of such a matrix at large values of 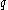 are diagonally dominant in the above sense.)
are diagonally dominant in the above sense.)
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is said to be diagonally dominant if for every row of the matrix, the magnitude of the diagonal entry in a row is larger than or equal to the sum of the magnitudes of all the other (non-diagonal) entries in that row. More precisely, the matrix A is diagonally dominant if
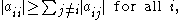
where aij denotes the entry in the ith row and jth column.
Note that this definition uses a weak inequality, and is therefore sometimes called weak diagonal dominance. If a strict inequality (>) is used, this is called strict diagonal dominance. The unqualified term diagonal dominance can mean both strict and weak diagonal dominance, depending on the context.
Variations
The definition in the first paragraph sums entries across rows. It is therefore sometimes called row diagonal dominance. If one changes the definition to sum down columns, this is called column diagonal dominance.If an irreducible
Irreducible (mathematics)
In mathematics, the concept of irreducibility is used in several ways.* In abstract algebra, irreducible can be an abbreviation for irreducible element; for example an irreducible polynomial....
matrix is weakly diagonally dominant, but in at least one row (or column) is strictly diagonally dominant, then the matrix is irreducibly diagonally dominant.
Examples
The matrix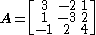
gives
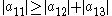 since
since 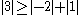
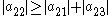 since
since 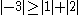
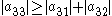 since
since 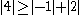 .
.Because the magnitude of each diagonal element is greater than or equal to the sum of the magnitude of other elements in the row, A is diagonally dominant.
The matrix
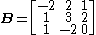
But here,
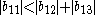 since
since 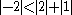
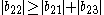 since
since 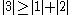
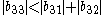 since
since 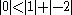 .
.Because
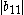 and
and 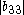 are less than the sum of the magnitude of other elements in their respective row, B is not diagonally dominant.
are less than the sum of the magnitude of other elements in their respective row, B is not diagonally dominant.The matrix
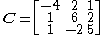
gives
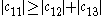 since
since 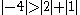
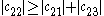 since
since 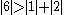
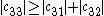 since
since 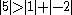 .
.Because the magnitude of each diagonal element is greater than the sum of the magnitude of the other elements in the row, C is strictly diagonally dominant.
Applications and properties
By the Gershgorin circle theoremGershgorin circle theorem
In mathematics, the Gershgorin circle theorem may be used to bound the spectrum of a square matrix. It was first published by the Belarusian mathematician Semyon Aranovich Gershgorin in 1931. The spelling of S. A...
, a strictly (or irreducibly) diagonally dominant matrix is non-singular. This result is known as the Levy–Desplanques theorem.
A Hermitian diagonally dominant matrix with real non-negative diagonal entries is positive semi-definite. If the symmetry requirement is eliminated, such a matrix is not necessarily positive semi-definite; however, the real parts of its eigenvalues are non-negative.
No (partial) pivoting is necessary for a strictly column diagonally dominant matrix when performing Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
(LU factorization).
The Jacobi
Jacobi method
In numerical linear algebra, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process...
and Gauss–Seidel methods for solving a linear system converge if the matrix is strictly (or irreducibly) diagonally dominant. In October 2010, researchers at Carnegie Mellon University
Carnegie Mellon University
Carnegie Mellon University is a private research university in Pittsburgh, Pennsylvania, United States....
announced that they have discovered a new algorithm for solving symmetric diagonally dominant linear systems.
Many matrices that arise in finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
s are diagonally dominant.
A slight variation on the idea of diagonal dominance is used to prove that the pairing on diagrams without loops in the Temperley–Lieb algebra is nondegenerate. For a matrix with polynomial entries, one sensible definition of diagonal dominance is if the highest power of
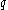 appearing in each row appears only on the diagonal. (The evaluations of such a matrix at large values of
appearing in each row appears only on the diagonal. (The evaluations of such a matrix at large values of 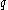 are diagonally dominant in the above sense.)
are diagonally dominant in the above sense.)
