
Jacques Touchard
Encyclopedia
Jacques Touchard was a French
mathematician
. In 1953, he proved that an odd perfect number
must be of the form 12k + 1 or 36k + 9. In combinatorics
and probability theory
, he introduced the Touchard polynomials. He is also known for his solution to the ménage problem
of counting seating arrangements in which men and women alternate and are not seated next to their spouses.
s
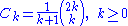
is apparently due to Touchard (according to Richard P. Stanley
, who mentions it in his panorama article "Exercises on Catalan and Related Numbers" giving an overwhelming plenitude of different definitions for the Catalan numbers).
For n ≥ 0 one has
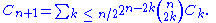
Using the generating function
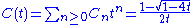
it can be proved by algebraic manipulations of generating series
that Touchard's identity is
equivalent to the functional equation

satisfied by the Catalan generating series C(t).
French people
The French are a nation that share a common French culture and speak the French language as a mother tongue. Historically, the French population are descended from peoples of Celtic, Latin and Germanic origin, and are today a mixture of several ethnic groups...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
. In 1953, he proved that an odd perfect number
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
must be of the form 12k + 1 or 36k + 9. In combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, he introduced the Touchard polynomials. He is also known for his solution to the ménage problem
Ménage problem
In combinatorial mathematics, the ménage problem or problème des ménages asks for the number of different ways in which it is possible to seat a set of heterosexual couples at a dining table so that men and women alternate and nobody sits next to his or her partner...
of counting seating arrangements in which men and women alternate and are not seated next to their spouses.
Touchard's Catalan identity
The following algebraic identity involving the Catalan numberCatalan number
In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
s
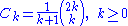
is apparently due to Touchard (according to Richard P. Stanley
Richard P. Stanley
Richard Peter Stanley is the Norman Levinson Professor of Applied Mathematics at the Massachusetts Institute of Technology, in Cambridge, Massachusetts. He received his Ph.D. at Harvard University in 1971 under the supervision of Gian-Carlo Rota...
, who mentions it in his panorama article "Exercises on Catalan and Related Numbers" giving an overwhelming plenitude of different definitions for the Catalan numbers).
For n ≥ 0 one has
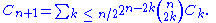
Using the generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
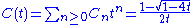
it can be proved by algebraic manipulations of generating series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
that Touchard's identity is
equivalent to the functional equation
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...

satisfied by the Catalan generating series C(t).

