Japanese theorem for concyclic quadrilaterals
Encyclopedia
In geometry
, the Japanese theorem states that the centers of the incircles of certain triangles inside a cyclic quadrilateral
are vertices of a rectangle.
Triangulating an arbitrary concyclic quadrilateral by its diagonals yields four overlapping triangles (each diagonal creates two triangles). The centers of the incircles of those triangles form a rectangle.
Specifically, let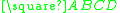
be an arbitrary concyclic quadrilateral and let be 
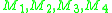the incenters of the triangles 
. Then the quadrilateral formed by 
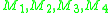is a rectangle.
Note that this theorem is easily extended to prove the Japanese theorem for cyclic polygons. To prove the quadrilateral case, simply construct the parallelogram tangent to the corners of the constructed rectangle, with sides parallel to the diagonals of the quadrilateral. The construction shows that the parallelogram is a rhombus, which is equivalent to showing that the sums of the radii of the incircles tangent to each diagonal are equal.
The quadrilateral case immediately proves the general case by induction on the set of triangulating partitions of a general polygon.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the Japanese theorem states that the centers of the incircles of certain triangles inside a cyclic quadrilateral
Cyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
are vertices of a rectangle.
Triangulating an arbitrary concyclic quadrilateral by its diagonals yields four overlapping triangles (each diagonal creates two triangles). The centers of the incircles of those triangles form a rectangle.
Specifically, let
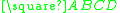be an arbitrary concyclic quadrilateral and let be 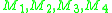the incenters of the triangles . Then the quadrilateral formed by 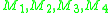is a rectangle.Note that this theorem is easily extended to prove the Japanese theorem for cyclic polygons. To prove the quadrilateral case, simply construct the parallelogram tangent to the corners of the constructed rectangle, with sides parallel to the diagonals of the quadrilateral. The construction shows that the parallelogram is a rhombus, which is equivalent to showing that the sums of the radii of the incircles tangent to each diagonal are equal.
The quadrilateral case immediately proves the general case by induction on the set of triangulating partitions of a general polygon.