
Johnson circles
Encyclopedia
In geometry
, a set of Johnson circles comprise three circle
s of equal radius
r sharing one common point of intersection H. In such a configuration the circles usually have a total of four intersections (points where at least two of them meet): the common point H that they all share, and for each of the three pairs of circles one more intersection point (referred here as their 2-wise intersection). If any two of the circles happen to just touch tangentially they only have H as a common point, and it will then be considered that H be their 2-wise intersection as well; if they should coincide we declare their 2-wise intersection be the point diametrically opposite H. The three 2-wise intersection points define the reference triangle of the figure.
Property 2 is also clear: for any circle of radius r, and any point P on it, the circle of radius 2r centered at P is tangent to the circle in its point opposite to P; this applies in particular to P=H, giving the anticomplementary circle C.
Property 3 in the formulation of the homothety immediately follows; the triangle of points of tangency is known as the anticomplementary triangle.
For properties 4 and 5, first observe that any two of the three Johnson circles are interchanged by the reflection in the line connecting H and their 2-wise intersection (or in their common tangent
at H if these points should coincide), and this reflection also interchanges the two vertices of the anticomplementary triangle lying on these circles. The 2-wise intersection point therefore is the midpoint of a side of the anticomplementary triangle, and H lies on the perpendicular bisector of this side. Now the midpoints of the sides of any triangle are the images of its vertices by a homothety with factor −½, centered at the barycenter of the triangle. Applied to the anticomplementary triangle, which is itself obtained from the Johnson triangle by a homothety with factor 2, it follows from composition of homotheties that the reference triangle is homothetic to the Johnson triangle by a factor −1. Since such a homothety is a congruence
, this gives property 5, and also the Johnson circles theorem since congruent triangles have circumscribed circle
s of equal radius.
For property 6, it was already established that the perpendicular bisectors of the sides of the anticomplementary triangle all pass through the point H; since that side is parallel to a side of the reference triangle, these perpendicular bisectors are also the altitude
s of the reference triangle.
Property 7 follows immediately from property 6 since the homothetic center whose factor is -1 must lie at the midpoint of the circumcenters O of the reference triangle and H of the Johnson triangle; the latter is the orthocenter of the reference triangle, and its nine-point center is known to be that midpoint. Since the central symmetry also maps the orthocenter of the reference triangle to that of the Johnson triangle, the homothetic center is also the nine-point center of the Johnson triangle.
There is also an algebraic proof of the Johnson circles theorem, using a simple vector computation. There are vectors ,
, 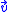 , and
, and 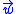 , all of length r, such that the Johnson circles are centered respectively at
, all of length r, such that the Johnson circles are centered respectively at 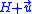 ,
, 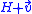 , and
, and 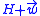 . Then the 2-wise intersection points are respectively
. Then the 2-wise intersection points are respectively 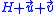 ,
, 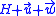 , and
, and 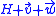 , and the point
, and the point 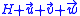 clearly has distance r to any of those 2-wise intersection points.
clearly has distance r to any of those 2-wise intersection points.
The Johnson triangle and its reference triangle share the same nine-point center, the same Euler line and the same nine-point circle
. The six points formed from the vertices of the reference triangle and its Johnson triangle all lie on the Johnson circumconic that is centred at the nine-point center and that has the point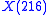 of the reference triangle as its perspector. The circumconic and the circumcircle share a fourth point,
of the reference triangle as its perspector. The circumconic and the circumcircle share a fourth point, 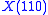 of the reference triangle.
of the reference triangle.
Finally there are two interesting and documented circumcubics that pass through the six vertices of the reference triangle and its Johnson triangle as well as the circumcenter, the orthocenter and the nine-point center. The first is known as the first Musselman cubic – . This cubic also passes through the six vertices of the medial triangle
. This cubic also passes through the six vertices of the medial triangle
and the medial triangle of the Johnson triangle. The second cubic is known as the Euler central cubic –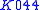 . This cubic also passes through the six vertices of the orthic triangle and the orthic triangle of the Johnson triangle.
. This cubic also passes through the six vertices of the orthic triangle and the orthic triangle of the Johnson triangle.
The X(i) point notation is the Clark Kimberling ETC
classification of triangle centers.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a set of Johnson circles comprise three circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s of equal radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
r sharing one common point of intersection H. In such a configuration the circles usually have a total of four intersections (points where at least two of them meet): the common point H that they all share, and for each of the three pairs of circles one more intersection point (referred here as their 2-wise intersection). If any two of the circles happen to just touch tangentially they only have H as a common point, and it will then be considered that H be their 2-wise intersection as well; if they should coincide we declare their 2-wise intersection be the point diametrically opposite H. The three 2-wise intersection points define the reference triangle of the figure.
Properties
- The centers of the Johnson circles lie on a circle of the same radius r as the Johnson circles centered at H. These centers form the Johnson triangle.
- The circle centered at H with radius 2r, known as the anticomplementary circle is tangent to each of the Johnson circles. The three tangent points are reflections of point H about the vertices of the Johnson triangle.
- The points of tangency between the Johnson circles and the anticomplementary circle form another triangle, called the anticomplementary triangle of the reference triangle. It is similarSimilarity (geometry)Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
to the Johnson triangle, and is homothetic by a factor 2 centered at H, their common circumcenter. - Johnson's theorem: The 2-wise intersection points of the Johnson circles (vertices of the reference triangle ABC) lie on a circle of the same radius r as the Johnson circles. This property is also well known in RomaniaRomaniaRomania is a country located at the crossroads of Central and Southeastern Europe, on the Lower Danube, within and outside the Carpathian arch, bordering on the Black Sea...
as The 5 lei coin problem of Gheoghe ŢiţeicaGheorghe TiteicaGheorghe Ţiţeica publishing as George or Georges Tzitzeica) was a Romanian mathematician with important contributions in geometry. He is recognized as the founder of the Romanian school of differential geometry....
. - The reference triangle is in fact congruentCongruence (geometry)In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
to the Johnson triangle, and is homothetic to it by a factor −1. - The point H is the orthocenter of the reference triangle and the circumcenter of the Johnson triangle.
- The homothetic center of the Johnson triangle and the reference triangle is their common nine-point center.
Proofs
Property 1 is obvious from the definition.Property 2 is also clear: for any circle of radius r, and any point P on it, the circle of radius 2r centered at P is tangent to the circle in its point opposite to P; this applies in particular to P=H, giving the anticomplementary circle C.
Property 3 in the formulation of the homothety immediately follows; the triangle of points of tangency is known as the anticomplementary triangle.
For properties 4 and 5, first observe that any two of the three Johnson circles are interchanged by the reflection in the line connecting H and their 2-wise intersection (or in their common tangent
Tangent lines to circles
In Euclidean plane geometry, tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs...
at H if these points should coincide), and this reflection also interchanges the two vertices of the anticomplementary triangle lying on these circles. The 2-wise intersection point therefore is the midpoint of a side of the anticomplementary triangle, and H lies on the perpendicular bisector of this side. Now the midpoints of the sides of any triangle are the images of its vertices by a homothety with factor −½, centered at the barycenter of the triangle. Applied to the anticomplementary triangle, which is itself obtained from the Johnson triangle by a homothety with factor 2, it follows from composition of homotheties that the reference triangle is homothetic to the Johnson triangle by a factor −1. Since such a homothety is a congruence
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
, this gives property 5, and also the Johnson circles theorem since congruent triangles have circumscribed circle
Circumscribed circle
In geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....
s of equal radius.
For property 6, it was already established that the perpendicular bisectors of the sides of the anticomplementary triangle all pass through the point H; since that side is parallel to a side of the reference triangle, these perpendicular bisectors are also the altitude
Altitude (triangle)
In geometry, an altitude of a triangle is a straight line through a vertex and perpendicular to a line containing the base . This line containing the opposite side is called the extended base of the altitude. The intersection between the extended base and the altitude is called the foot of the...
s of the reference triangle.
Property 7 follows immediately from property 6 since the homothetic center whose factor is -1 must lie at the midpoint of the circumcenters O of the reference triangle and H of the Johnson triangle; the latter is the orthocenter of the reference triangle, and its nine-point center is known to be that midpoint. Since the central symmetry also maps the orthocenter of the reference triangle to that of the Johnson triangle, the homothetic center is also the nine-point center of the Johnson triangle.
There is also an algebraic proof of the Johnson circles theorem, using a simple vector computation. There are vectors
 ,
, 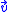 , and
, and 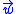 , all of length r, such that the Johnson circles are centered respectively at
, all of length r, such that the Johnson circles are centered respectively at 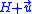 ,
, 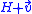 , and
, and 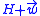 . Then the 2-wise intersection points are respectively
. Then the 2-wise intersection points are respectively 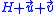 ,
, 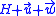 , and
, and 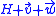 , and the point
, and the point 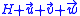 clearly has distance r to any of those 2-wise intersection points.
clearly has distance r to any of those 2-wise intersection points.Further properties
The three Johnson circles can be considered the reflections of the circumcircle of the reference triangle about each of the three sides of the reference triangle. Furthermore, under the reflections about the three sides of the reference triangle, its orthocenter H maps onto certain points on the circumcircle of the reference triangle that form the vertices of the circum-orthic triangle, and its circumcenter maps onto the vertices of the Johnson triangle.The Johnson triangle and its reference triangle share the same nine-point center, the same Euler line and the same nine-point circle
Nine-point circle
In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant points defined from the triangle...
. The six points formed from the vertices of the reference triangle and its Johnson triangle all lie on the Johnson circumconic that is centred at the nine-point center and that has the point
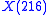 of the reference triangle as its perspector. The circumconic and the circumcircle share a fourth point,
of the reference triangle as its perspector. The circumconic and the circumcircle share a fourth point, 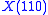 of the reference triangle.
of the reference triangle.Finally there are two interesting and documented circumcubics that pass through the six vertices of the reference triangle and its Johnson triangle as well as the circumcenter, the orthocenter and the nine-point center. The first is known as the first Musselman cubic –
 . This cubic also passes through the six vertices of the medial triangle
. This cubic also passes through the six vertices of the medial triangleMedial triangle
The medial triangle of a triangle ABC is the triangle with vertices at the midpoints of the triangle's sides AB, AC and BC....
and the medial triangle of the Johnson triangle. The second cubic is known as the Euler central cubic –
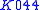 . This cubic also passes through the six vertices of the orthic triangle and the orthic triangle of the Johnson triangle.
. This cubic also passes through the six vertices of the orthic triangle and the orthic triangle of the Johnson triangle.The X(i) point notation is the Clark Kimberling ETC
Encyclopedia of Triangle Centers
The Encyclopedia of Triangle Centers is an on-line list of more than 3,000 points or "centers" associated with the geometry of a triangle. It is maintained by Clark Kimberling, Professor of Mathematics at the University of Evansville....
classification of triangle centers.

