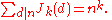Jordan's totient function
Encyclopedia
In number theory
, Jordan's totient function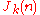 of a positive integer n is the number of k-tuples of positive integers all less than or equal to n that form a coprime
of a positive integer n is the number of k-tuples of positive integers all less than or equal to n that form a coprime
(k + 1)-tuple together with n. This is a generalisation of Euler's totient function, which is J1. The function is named after Camille Jordan
.
and may be evaluated as
which may be written in the language of Dirichlet convolution
s as
and via Möbius inversion
as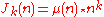 .
.
Since the Dirichlet generating function of μ is 1/ζ(s) and the
Dirichlet generating function of nk is ζ(s-k), the series for
Jk becomes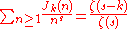 .
.
and by inspection of the definition (recognizing that each factor in the product
over the primes is a cyclotomic polynomial of p-k), the arithmetic functions
defined by or
or 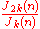
can also be shown to be integer-valued multiplicative functions.
J2 in ,
J3 in ,
J4 in ,
J5 in ,
J6 up to J10 in
up to .
Multiplicative functions defined by ratios are
J2(n)/J1(n) in ,
J3(n)/J1(n) in ,
J4(n)/J1(n) in ,
J5(n)/J1(n) in ,
J6(n)/J1(n) in ,
J7(n)/J1(n) in ,
J8(n)/J1(n) in ,
J9(n)/J1(n) in ,
J10(n)/J1(n) in ,
J11(n)/J1(n) in .
Examples of the ratios J2k(n)/Jk(n) are
J4(n)/J2(n) in ,
J6(n)/J3(n) in ,
and
J8(n)/J4(n) in .
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Jordan's totient function
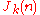 of a positive integer n is the number of k-tuples of positive integers all less than or equal to n that form a coprime
of a positive integer n is the number of k-tuples of positive integers all less than or equal to n that form a coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
(k + 1)-tuple together with n. This is a generalisation of Euler's totient function, which is J1. The function is named after Camille Jordan
Camille Jordan
Marie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
.
Definition
Jordan's totient function is multiplicativeMultiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
and may be evaluated as

Properties
which may be written in the language of Dirichlet convolution
Dirichlet convolution
In mathematics, the Dirichlet convolution is a binary operation defined for arithmetic functions; it is important in number theory. It was developed by Johann Peter Gustav Lejeune Dirichlet, a German mathematician.-Definition:...
s as
and via Möbius inversion
Möbius inversion formula
In mathematics, the classic Möbius inversion formula was introduced into number theory during the 19th century by August Ferdinand Möbius. Other Möbius inversion formulas are obtained when different local finite partially ordered sets replace the classic case of the natural numbers ordered by...
as
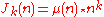 .
.Since the Dirichlet generating function of μ is 1/ζ(s) and the
Dirichlet generating function of nk is ζ(s-k), the series for
Jk becomes
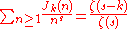 .
.
- The average orderAverage order of an arithmetic functionIn number theory, the average order of an arithmetic function is some simpler or better-understood function which takes the same values "on average".Let f be an arithmetic function...
of Jk(n) is c nk for some c. - The Dedekind psi function is
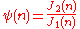 ,
,
and by inspection of the definition (recognizing that each factor in the product
over the primes is a cyclotomic polynomial of p-k), the arithmetic functions
defined by
 or
or 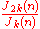
can also be shown to be integer-valued multiplicative functions.
Examples
Explicit lists in the OEIS areJ2 in ,
J3 in ,
J4 in ,
J5 in ,
J6 up to J10 in
up to .
Multiplicative functions defined by ratios are
J2(n)/J1(n) in ,
J3(n)/J1(n) in ,
J4(n)/J1(n) in ,
J5(n)/J1(n) in ,
J6(n)/J1(n) in ,
J7(n)/J1(n) in ,
J8(n)/J1(n) in ,
J9(n)/J1(n) in ,
J10(n)/J1(n) in ,
J11(n)/J1(n) in .
Examples of the ratios J2k(n)/Jk(n) are
J4(n)/J2(n) in ,
J6(n)/J3(n) in ,
and
J8(n)/J4(n) in .