KMS state
Encyclopedia
In the statistical mechanics
of quantum mechanical
systems and quantum field theory
, the properties of a system in thermal equilibrium can be described by a mathematical object called a Kubo
-Martin-Schwinger
state or, more commonly, a KMS state.
, in which one does not encounter complications like phase transition
s or spontaneous symmetry breaking
. The density matrix
of a thermal state is given by
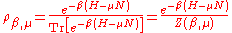
where H is the Hamiltonian
operator
and N is the particle number operator
(or charge
operator, if we wish to be more general) and
is the partition function
. We assume that N commutes with H, or in other words, that particle number is conserved
.
In the Heisenberg picture
, the density matrix does not change with time, but the operators are time-dependent. In particular, translating an operator A by τ into the future gives the operator
.
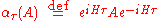A combination of time translation with an internal symmetry "rotation" gives the more general
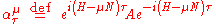
A bit of algebraic manipulation shows that the expected value
s
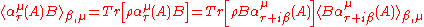
for any two operators A and B and any real τ (we are working with finite-dimensional Hilbert spaces after all). We used the fact that the density matrix commutes with any function of (H-μN) and that the trace
is cyclic.
As hinted at earlier, with infinite dimensional Hilbert spaces, we run into a lot of problems like phase transitions, spontaneous symmetry breaking, operators which aren't trace class
, divergent partition functions, etc..
The complex functions of z,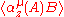
converges in the complex strip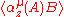 
whereas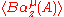
converges in the complex strip
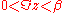
if we make certain technical assumptions like the spectrum of H-μN is bounded from below and its density doesn't increase exponentially (see Hagedorn temperature
). If the functions converge, then they have to be analytic
within the strip they are defined over as their derivatives,
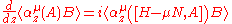
and
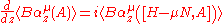
exist.
However, we can still define a KMS state as any state satisfying
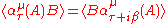
with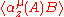
and 
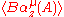being analytic functions of z within their domain strips.
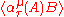and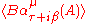 
are the boundary distribution
values of the analytic functions in question.
This gives the right large volume, large particle number thermodynamic limit. If there is a phase transition or spontaneous symmetry breaking, the KMS state isn't unique.
The density matrix of a KMS state is related to unitary transformation
s involving time translations (or time translations and an internal symmetry transformation for nonzero chemical potentials) via the Tomita–Takesaki theory.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
of quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
systems and quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the properties of a system in thermal equilibrium can be described by a mathematical object called a Kubo
Ryogo Kubo
was a Japanese mathematical physicist, best known for his works in statistical physics and non-equilibrium statistical mechanics.In the early 1950s, Kubo transformed research into the linear response properties of near-equilibrium condensed-matter systems, in particular the understanding of...
-Martin-Schwinger
Julian Schwinger
Julian Seymour Schwinger was an American theoretical physicist. He is best known for his work on the theory of quantum electrodynamics, in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order.Schwinger is recognized as one of the...
state or, more commonly, a KMS state.
Preliminaries
The simplest case to study is that of a finite-dimensional Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, in which one does not encounter complications like phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
s or spontaneous symmetry breaking
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
. The density matrix
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
of a thermal state is given by
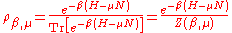
where H is the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
operator
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
and N is the particle number operator
Particle number operator
In quantum mechanics, for systems where the total number of particles may not be preserved, the number operator is the observable that counts the number of particles.The number operator acts on Fock space...
(or charge
Charge (physics)
In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...
operator, if we wish to be more general) and
is the partition function
Partition function (quantum field theory)
In quantum field theory, we have a generating functional, Z[J] of correlation functions and this value, called the partition function is usually expressed by something like the following functional integral:...
. We assume that N commutes with H, or in other words, that particle number is conserved
Conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
.
In the Heisenberg picture
Heisenberg picture
In physics, the Heisenberg picture is a formulation of quantum mechanics in which the operators incorporate a dependency on time, but the state vectors are time-independent. It stands in contrast to the Schrödinger picture in which the operators are constant and the states evolve in time...
, the density matrix does not change with time, but the operators are time-dependent. In particular, translating an operator A by τ into the future gives the operator
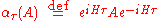.A combination of time translation with an internal symmetry "rotation" gives the more general
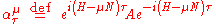
A bit of algebraic manipulation shows that the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
s
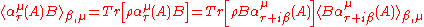
for any two operators A and B and any real τ (we are working with finite-dimensional Hilbert spaces after all). We used the fact that the density matrix commutes with any function of (H-μN) and that the trace
Trace class
In mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
is cyclic.
As hinted at earlier, with infinite dimensional Hilbert spaces, we run into a lot of problems like phase transitions, spontaneous symmetry breaking, operators which aren't trace class
Trace class
In mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
, divergent partition functions, etc..
The complex functions of z,
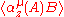converges in the complex strip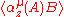 whereas
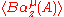converges in the complex strip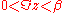if we make certain technical assumptions like the spectrum of H-μN is bounded from below and its density doesn't increase exponentially (see Hagedorn temperature
Hagedorn temperature
The Hagedorn temperature in theoretical physics is the temperature above which the partition sum diverges in a system with exponential growth in the density of states. It is named after German physicist Rolf Hagedorn.Phase transitions The Hagedorn temperature in theoretical physics is the...
). If the functions converge, then they have to be analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
within the strip they are defined over as their derivatives,
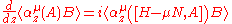
and
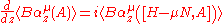
exist.
However, we can still define a KMS state as any state satisfying
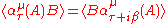
with
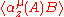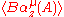and being analytic functions of z within their domain strips. 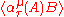and 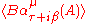are the boundary distributionDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
values of the analytic functions in question.
This gives the right large volume, large particle number thermodynamic limit. If there is a phase transition or spontaneous symmetry breaking, the KMS state isn't unique.
The density matrix of a KMS state is related to unitary transformation
Unitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
s involving time translations (or time translations and an internal symmetry transformation for nonzero chemical potentials) via the Tomita–Takesaki theory.