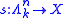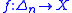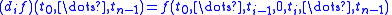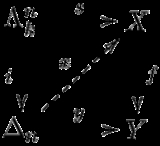
Kan fibration
Encyclopedia
In mathematics, Kan complexes and Kan fibrations are part of the theory of simplicial set
s. Kan fibrations are the fibrations of the standard model category
for simplicial sets and are therefore of fundamental importance. Kan complexes are the fibrant object
s in this model category. The name is in honor of Daniel Kan
.
 -simplex,
-simplex, 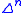 , is the representable simplicial set
, is the representable simplicial set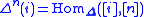
Applying the geometric realization functor to this simplicial set gives a space homeomorphic to the topological standard -simplex: the convex subspace of ℝn+1 consisting of all points
-simplex: the convex subspace of ℝn+1 consisting of all points 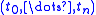 such that the coordinates are non-negative and sum to 1.
such that the coordinates are non-negative and sum to 1.
For each k ≤ n, this has a subcomplex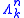 , the k-th horn inside
, the k-th horn inside 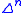 , corresponding to the boundary of the n-simplex, with the k-th face removed. This may be formally defined in various ways, as for instance the union of the images of the n maps
, corresponding to the boundary of the n-simplex, with the k-th face removed. This may be formally defined in various ways, as for instance the union of the images of the n maps 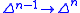 corresponding to all the other faces of
corresponding to all the other faces of 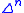 . Horns of the form
. Horns of the form 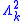 sitting inside
sitting inside 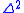 look like the black V at the top of the image to the right. If
look like the black V at the top of the image to the right. If  is a simplicial set, then maps
is a simplicial set, then maps
correspond to collections of
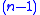 -simplices satisfying a compatibility condition. Explicitly, this condition can be written as follows. Write the
-simplices satisfying a compatibility condition. Explicitly, this condition can be written as follows. Write the  -simplices as a list
-simplices as a list 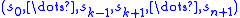 and require that
and require that
These conditions are satisfied for the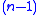 -simplices of
-simplices of 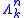 sitting inside
sitting inside 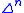 .
.
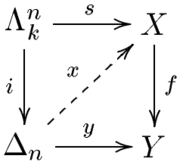 A map of simplicial sets
A map of simplicial sets 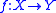 is a Kan fibration if, for any
is a Kan fibration if, for any  , and for any maps
, and for any maps 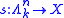 and
and 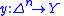 such that
such that  , there exists a map
, there exists a map 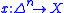 such that
such that 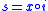 and
and
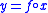 . Stated this way, the definition is very similar to that of fibration
. Stated this way, the definition is very similar to that of fibration
s in topology
(see also homotopy lifting property
), whence the name "fibration".
Using the correspondence between -simplices of a simplicial set
-simplices of a simplicial set  and morphisms
and morphisms 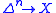 (a consequence of the Yoneda lemma
(a consequence of the Yoneda lemma
), this definition can be written in terms of simplices. The image of the map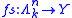 can be thought of as a horn as described above. Asking that
can be thought of as a horn as described above. Asking that 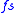 factors through
factors through 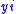 corresponds to requiring that there is an
corresponds to requiring that there is an  -simplex in
-simplex in  whose faces make up the horn from
whose faces make up the horn from 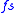 (together with one other face). Then the required map
(together with one other face). Then the required map 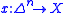 corresponds to a simplex in
corresponds to a simplex in  whose faces include the horn from
whose faces include the horn from  . The diagram to the right is an example in two dimensions. Since the black V in the lower diagram is filled in by the blue
. The diagram to the right is an example in two dimensions. Since the black V in the lower diagram is filled in by the blue 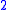 -simplex, if the black V above maps down to it then the striped blue
-simplex, if the black V above maps down to it then the striped blue 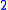 -simplex has to exist, along with the dotted blue
-simplex has to exist, along with the dotted blue 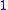 -simplex, mapping down in the obvious way.
-simplex, mapping down in the obvious way.
A simplicial set X is called a Kan complex if the map from X to 1, the one-point simplicial set, is a Kan fibration. In the model category
for simplicial sets,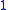 is the terminal object and so an Kan complex is exactly the same as a fibrant object
is the terminal object and so an Kan complex is exactly the same as a fibrant object
.
. Given a space , define a singular
, define a singular  -simplex of X to be a continuous map from the standard topological
-simplex of X to be a continuous map from the standard topological  -simplex (as described above) to
-simplex (as described above) to  ,
,
Taking the set of these maps for all non-negative gives a graded set,
gives a graded set,
To make this into a simplicial set, define face maps by
by
and degeneracy maps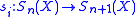 by
by
Since the union of any faces of
faces of 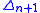 is a strong deformation retract
is a strong deformation retract
of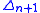 , any continuous function defined on these faces can be extended to
, any continuous function defined on these faces can be extended to 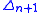 , which shows that
, which shows that 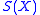 is a Kan complex.
is a Kan complex.
It can be shown that the simplicial set underlying a simplicial group
is always fibrant.
s of a fibrant simplicial set may be defined combinatorially, using horns, in a way that agrees with
the homotopy groups of the topological space which realizes it.
Simplicial set
In mathematics, a simplicial set is a construction in categorical homotopy theory which is a purely algebraic model of the notion of a "well-behaved" topological space...
s. Kan fibrations are the fibrations of the standard model category
Model category
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms called 'weak equivalences', 'fibrations' and 'cofibrations'. These abstract from a conventional homotopy category, of topological spaces or of chain complexes...
for simplicial sets and are therefore of fundamental importance. Kan complexes are the fibrant object
Fibrant object
In mathematics, specifically in homotopy theory in the context of a model category M, a fibrant object A of M is an object that has a fibration to the terminal object of the category.-Properties:...
s in this model category. The name is in honor of Daniel Kan
Daniel Kan
Daniel Marinus Kan is a mathematician working in homotopy theory. He has been a prolific contributor to the field for the last five decades, having authored or coauthored several dozen research papers and monographs. The general theme of his career has been abstract homotopy theory.He is an...
.
Definition
For each n ≥ 0, recall that the standard -simplex,
-simplex, 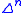 , is the representable simplicial set
, is the representable simplicial set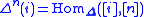
Applying the geometric realization functor to this simplicial set gives a space homeomorphic to the topological standard
 -simplex: the convex subspace of ℝn+1 consisting of all points
-simplex: the convex subspace of ℝn+1 consisting of all points 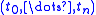 such that the coordinates are non-negative and sum to 1.
such that the coordinates are non-negative and sum to 1.For each k ≤ n, this has a subcomplex
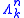 , the k-th horn inside
, the k-th horn inside 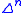 , corresponding to the boundary of the n-simplex, with the k-th face removed. This may be formally defined in various ways, as for instance the union of the images of the n maps
, corresponding to the boundary of the n-simplex, with the k-th face removed. This may be formally defined in various ways, as for instance the union of the images of the n maps 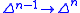 corresponding to all the other faces of
corresponding to all the other faces of 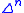 . Horns of the form
. Horns of the form 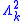 sitting inside
sitting inside 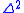 look like the black V at the top of the image to the right. If
look like the black V at the top of the image to the right. If  is a simplicial set, then maps
is a simplicial set, then maps
correspond to collections of

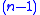 -simplices satisfying a compatibility condition. Explicitly, this condition can be written as follows. Write the
-simplices satisfying a compatibility condition. Explicitly, this condition can be written as follows. Write the  -simplices as a list
-simplices as a list 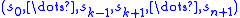 and require that
and require that
-
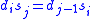 for all
for all  with
with  .
.
These conditions are satisfied for the
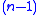 -simplices of
-simplices of 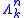 sitting inside
sitting inside 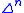 .
.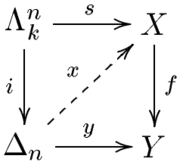
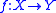 is a Kan fibration if, for any
is a Kan fibration if, for any  , and for any maps
, and for any maps 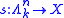 and
and 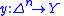 such that
such that  , there exists a map
, there exists a map 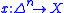 such that
such that 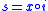 and
and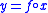 . Stated this way, the definition is very similar to that of fibration
. Stated this way, the definition is very similar to that of fibrationFibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
s in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
(see also homotopy lifting property
Homotopy lifting property
In mathematics, in particular in homotopy theory within algebraic topology, the homotopy lifting property is a technical condition on a continuous function from a topological space E to another one, B...
), whence the name "fibration".
Using the correspondence between
 -simplices of a simplicial set
-simplices of a simplicial set  and morphisms
and morphisms 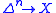 (a consequence of the Yoneda lemma
(a consequence of the Yoneda lemmaYoneda lemma
In mathematics, specifically in category theory, the Yoneda lemma is an abstract result on functors of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem from group theory...
), this definition can be written in terms of simplices. The image of the map
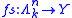 can be thought of as a horn as described above. Asking that
can be thought of as a horn as described above. Asking that 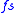 factors through
factors through 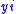 corresponds to requiring that there is an
corresponds to requiring that there is an  -simplex in
-simplex in  whose faces make up the horn from
whose faces make up the horn from 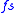 (together with one other face). Then the required map
(together with one other face). Then the required map 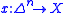 corresponds to a simplex in
corresponds to a simplex in  whose faces include the horn from
whose faces include the horn from  . The diagram to the right is an example in two dimensions. Since the black V in the lower diagram is filled in by the blue
. The diagram to the right is an example in two dimensions. Since the black V in the lower diagram is filled in by the blue 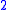 -simplex, if the black V above maps down to it then the striped blue
-simplex, if the black V above maps down to it then the striped blue 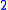 -simplex has to exist, along with the dotted blue
-simplex has to exist, along with the dotted blue 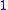 -simplex, mapping down in the obvious way.
-simplex, mapping down in the obvious way.A simplicial set X is called a Kan complex if the map from X to 1, the one-point simplicial set, is a Kan fibration. In the model category
Model category
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms called 'weak equivalences', 'fibrations' and 'cofibrations'. These abstract from a conventional homotopy category, of topological spaces or of chain complexes...
for simplicial sets,
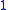 is the terminal object and so an Kan complex is exactly the same as a fibrant object
is the terminal object and so an Kan complex is exactly the same as a fibrant objectFibrant object
In mathematics, specifically in homotopy theory in the context of a model category M, a fibrant object A of M is an object that has a fibration to the terminal object of the category.-Properties:...
.
Examples
An important example comes from the singular simplices used to define singular homologySingular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
. Given a space
 , define a singular
, define a singular  -simplex of X to be a continuous map from the standard topological
-simplex of X to be a continuous map from the standard topological  -simplex (as described above) to
-simplex (as described above) to  ,
,
Taking the set of these maps for all non-negative
 gives a graded set,
gives a graded set,
-
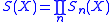 .
.
To make this into a simplicial set, define face maps
 by
by
and degeneracy maps
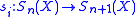 by
by
-
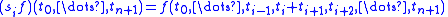 .
.
Since the union of any
 faces of
faces of 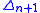 is a strong deformation retract
is a strong deformation retractDeformation retract
In topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
of
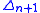 , any continuous function defined on these faces can be extended to
, any continuous function defined on these faces can be extended to 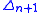 , which shows that
, which shows that 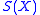 is a Kan complex.
is a Kan complex.It can be shown that the simplicial set underlying a simplicial group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is always fibrant.
Applications
The homotopy groupHomotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s of a fibrant simplicial set may be defined combinatorially, using horns, in a way that agrees with
the homotopy groups of the topological space which realizes it.